Итак, дело дошло до скользящего среднего (moving average, MA). Модель скользящего среднего — вещь совершенно не сложная, однако, как и все остальные модели прогнозирования или их составляющие, имеет целый ряд нюансов. Например, Википедия содержит в себе весьма громоздкое описание указанной модели, однако я не стану тут так подробно говорить об ней, но постараюсь кратко изложить основную ее идею.
Часто случается, что в исследуемом процессе имеются выбросы. Как правило, они весьма сложно исследуются. Очевидно, что подобные выбросы дурно влияют на ближайшие к ним прогнозные значения.
Ниже на графике представлен временной ряд цен рынка на сутки вперед (РСВ). Представим, что мы имеем фактические значения данного временного ряда до дня №2 и ранее, а спрогнозировать нам нужно значения в день №3. Совершенно очевидно, что если временной ряд регулярный, то выбросы дня №2 самым дурными образом скажутся на вычисленных значениях, если эти пики не сгладить.
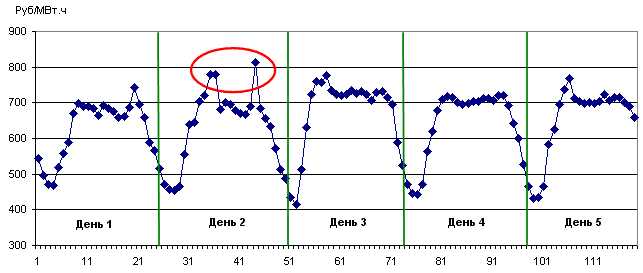
Для сглаживания подобных пиков и применяется модель скользящего среднего, которая, по сути дела, представляет собою простой фильтр низких частот.
Скользящее среднее второго порядка, которое принято обозначать как MA(2) для временного ряда Z(t) вычисляется следующим образом:
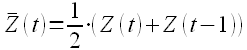
Скользящее среднее третьего порядка MA(3) вычисляется аналогично:
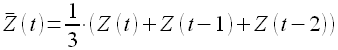
Скользящее среднее пятого порядка MA(5):
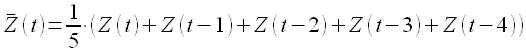
Таким образом, для скользящего среднего порядка p легко написать следующую формулу:
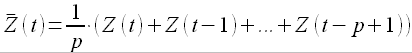
То есть скользящее среднее для момента t является алгебраическим средним нескольких предыдущих значений исходного временного ряда Z(t). На следующем графике представлен исходный временной ряд, а также MA(2) и MA(5). Обратите внимание на то, каким образом модель скользящего среднего влияет на выбросы в трех часах дня №2. Заметно, что выбросы существенно сгладились, однако весь остальной профиль временного ряда MA существенно не отличается от исходного, только несколько сдвинут по фазе. Такой сдвиг по фазе легко устранить обычным сдвигом значений ряда.
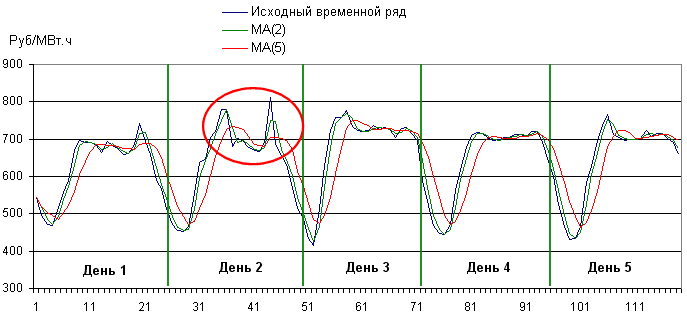
Таким образом, ясно, что скользящее среднее представляет собой фильтр, который позволяет сглаживать выбросы временного ряда, которые, в свою очередь, спрогнозировать достаточно сложно или вовсе невозможно.
У модели скользящего среднего множество нюансов, с которыми вы можете ознакомиться самостоятельно.
Тут чтото не то..
"метод скользящего среднего" - по сути простое сглажевание, работает как вы описали
а "МА(n) - модель скользящего среднего" - это когда мы пытаемся на основе отклоений построить регрессию, тоесть сначала используя PACF - находим кореляцию между отклоениями, например на лаге 1 и 2 она есть - тоесть у нас будет уравнение с 2 здвигами .. далее строим регрессию, как обычную по сути только на основе отклонений. Суть такова что есть отклонения которые мы неможем предсказать ... PACF нам говорит что есть закономерность .. и тебе стоит построить твое модель с меньшими квадратами оклонений