Модель авторегрессии
Предположим, у нас имеется временной ряд Z(t), представленный на рисунке ниже. Нужно вычислить будущее значение временного ряда в точке №41, то есть значение Z(41) (красный цвет) на основании 40 предыдущих точек Z(1), Z(2),…,Z(40) с использованием модели авторегрессии.

Формула для определения Z(41) выглядит следующим образом и называется авторегрессией порядка p:
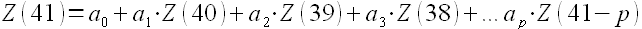
В это формуле мы знаем значения Z(40), Z(39), Z(38) и т.д., но не знаем коэффициенты a. Как их определить?
Если для Z(41) работает такая зависимость, значит, она работает и для предыдущих точек, т.е. мы можем получить систему уравнений:
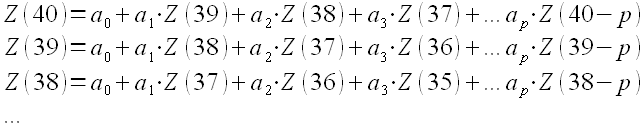
В этой системе уравнений мы знаем все значения Z(t), а, следовательно, можем легко определить коэффициенты a. Самый легкий способ определения коэффициентов - использование метода наименьших квадратов.
Два важных вопроса, которые нужно решить при использовании модели авторегрессии:
- Каков должен быть порядок p?
- Сколько уравнений нужно добавлять в матрицу, чтобы найденные коэффициенты авторегрессии a давали максимально точный прогноз?
Однозначных ответов на эти вопросы нет. Исследование функции автокорреляции для определения p на сегодняшний день отошло в прошлое, так как длина временных рядов имеет сотни и тысячи значений. Количество принимаемых в расчет уравнений часто зависит от сезонности временного ряда. Ответы на эти вопросы и должен найти разработчик данной модели, чтобы заставить ее прогнозировать надежно!
Модель авторегрессии с одной стороны довольно проста, так как принцип ее работы понятен и нагляден; с другой - сложна тем, что в ней имеет место множество нюансов, которые требуют кропотливого труда разработчика. Однако, не смотря на все нюансы, рассмотренная модель является частью большой модели ARIMAX, которая на сегодняшний день чрезвычайно популярна для решения задач прогнозирования временных рядов.