Скачать полный текст диссертации в формате PDF (2.9 Мб).
Простейший пример реализации в MATLAB рассмотренной ниже модели прогнозирования временных рядов с подробными комментариями выложен по ссылке Модель прогнозирования временных рядов по выборке максимального подобия: пояснение и пример.
Глава 2. Модели экстраполяции временных рядов по выборке максимального подобия
2.1. Модель без учета внешних факторов
2.1.1. Выборки временного ряда
2.1.2. Аппроксимация выборки
2.1.3. Подобие выборок
2.1.4. Описание модели экстраполяции
2.2. Модель с учетом внешних факторов
2.2.1. Выборки временных рядов
2.2.2. Аппроксимация выборки
2.2.3. Подобие выборок
2.2.4. Описание модели
2.3. Варианты моделей по выборке максимального подобия
2.4. Выводы
2.1. Модель без учета внешних факторов
2.1.1. Выборки временного ряда
Пусть задан временной ряд Z(t) = Z(1), Z(1),...,Z(T). Набор последовательных значений 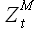 = Z(t), Z(t+1),...,Z(t+M-1), лежащий внутри исходного временного ряда, назовем выборкой длины M с моментом начала отчета t; M = {1,2,..,T}, t = {1,2,..,T-M+1}. Фактически выборкой является кусочек временного ряда, имеющий точку начала отсчета и длину.
= Z(t), Z(t+1),...,Z(t+M-1), лежащий внутри исходного временного ряда, назовем выборкой длины M с моментом начала отчета t; M = {1,2,..,T}, t = {1,2,..,T-M+1}. Фактически выборкой является кусочек временного ряда, имеющий точку начала отсчета и длину.
Две выборки одинаковой длины, принадлежащие одному временному ряду, обозначим через временную задержку k: 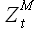 = Z(t),...,Z(t+M-1) и
= Z(t),...,Z(t+M-1) и 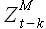 = Z(t-k),...,Z(t+M-k-1); k = {1,2,..,t-1}. На рисунках (2.1),(2.2),(2.3),(2.4) показаны выборки различных временных рядов.
= Z(t-k),...,Z(t+M-k-1); k = {1,2,..,t-1}. На рисунках (2.1),(2.2),(2.3),(2.4) показаны выборки различных временных рядов.
В работе [40] сформулирован подход к моделированию временных рядов по помощи выборок: «Pattern modelling refers to the process of describing the time series as a series of patterns». (Моделирование временных рядов при помощи выборок основано на предположении, что временной ряд представляет собой последовательность выборок.)
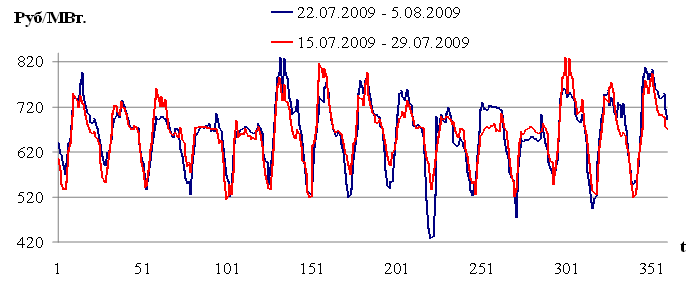
Рис. 2.1. Цена на электроэнергию европейской территории РФ
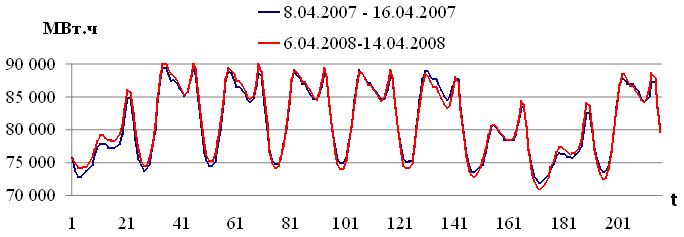
Рис. 2.2. Энергопотребление европейской территории РФ
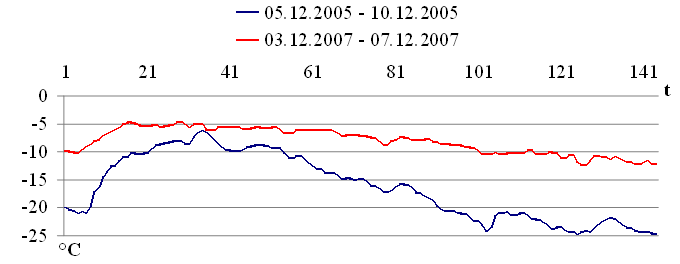
Рис. 2.3. Температура воздуха Новосибирской области
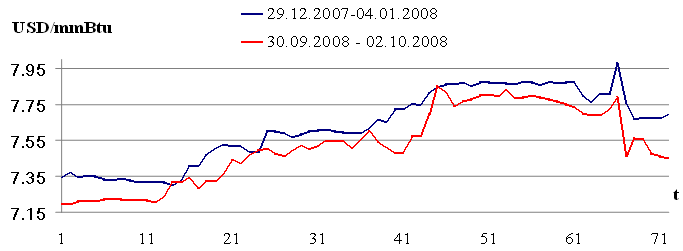
Рис. 2.4. Цена на природный газ на NYMEX
На рисунках 2.1 — 2.4 изображены выборки временных рядов, которые иллюстрируют свойство выборок, сформулированное в работе [42]: «Pieces of time series in the past might have a resemblance to pieces in the future». (Фактические выборки временного ряда могут иметь подобие с будущими выборками). Указанное свойство выборок будет использовано для построения модели прогнозирования.
В настоящем разделе сначала рассматривается задача аппроксимации одной выборки при помощи другой, а затем результаты аппроксимации применяются для построения модели прогнозирования временного ряда.
2.1.2. Аппроксимация выборки
Для расчетов перейдем к векторному обозначению выборки 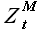 = (Z(t),Z(t+1),...,Z(t+M-1))Tи временного ряда
= (Z(t),Z(t+1),...,Z(t+M-1))Tи временного ряда 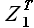 = (Z(1),Z(2),...,Z(T))T. Здесь и далее, говоря о выборках временного ряда будем использовать обозначение
= (Z(1),Z(2),...,Z(T))T. Здесь и далее, говоря о выборках временного ряда будем использовать обозначение 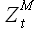 , говоря о векторах, соответствующих указанным выборкам, будем писать жирную
, говоря о векторах, соответствующих указанным выборкам, будем писать жирную 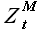 .
.
Используя свойство выборок повторяться, аппроксимируем выборку 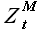 при помощи выборки
при помощи выборки 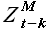 следующим образом
следующим образом
Здесь α1 и α0 — коэффициенты, IM — единичный вектор, EM — вектор значений ошибок аппроксимации. Выражение (2.1) можно переписать в виде
В формуле (2.2) 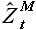 — аппроксимированные значения выборки
— аппроксимированные значения выборки 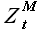 . Здесь и далее, говоря о вычисляемых (модельных) значениях выборки
. Здесь и далее, говоря о вычисляемых (модельных) значениях выборки 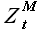 будем использовать обозначение
будем использовать обозначение 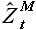 (с крышечкой).
(с крышечкой).
Постановка задачи аппроксимации выборки. Пусть дана функциональная зависимость выборок (2.2). Необходимо определить такие значения α1 и α0, чтобы квадрат отклонений модельных значений выборки 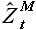 от фактических
от фактических 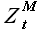 был минимален
был минимален
После нахождения коэффициентов α1 и α0, необходимо оценить вектор ошибок EM.
Решение. Пусть дана линейная зависимость (2.1), тогда функция ошибки аппроксимации 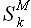 для выборок
для выборок 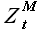 и
и 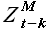 с задержкой k имеет вид
с задержкой k имеет вид
Функция 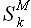 называется функцией суммы квадратов (sum of squares function) [19]. Задача состоит в том, чтобы подобрать такие значения α1 и α0, чтобы при подстановке их в (2.4) было получено минимальное возможное значение
называется функцией суммы квадратов (sum of squares function) [19]. Задача состоит в том, чтобы подобрать такие значения α1 и α0, чтобы при подстановке их в (2.4) было получено минимальное возможное значение 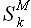 (α1, α0). Рисунок 2.5 иллюстрирует определение функции суммы квадратов.
(α1, α0). Рисунок 2.5 иллюстрирует определение функции суммы квадратов.
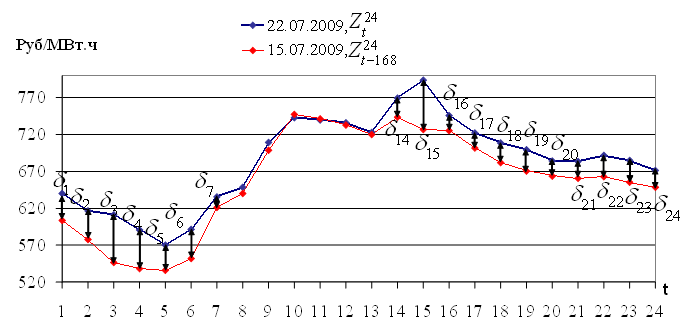
Рис. 2.5. Определение функции суммы квадратов по выражению (2.4)
Решим задачу при помощи метода наименьших квадратов, подробно описанного в работе [19]. После ряда преобразований задача сводится к решению матричного уравнения
Решая матричное уравнение (2.5), определяем значения коэффициентов α1 и α0, соответствующие минимуму функции 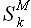 (α1, α0). Уравнение (2.5) может быть решено любым известным методом. Исходные матрицы являются квадратными и решение может быть найдено, например, при помощи обратной матрицы
(α1, α0). Уравнение (2.5) может быть решено любым известным методом. Исходные матрицы являются квадратными и решение может быть найдено, например, при помощи обратной матрицы
Оценка ошибки аппроксимации. Ошибка определяется по формуле
В настоящее время точность моделирования временных рядов EM принято оценивать при помощи двух показателей [28]:
- средняя абсолютная ошибка (mean absolute error, MAE)
- средняя абсолютная ошибка в процентах, (mean absolute percentage error, MAPE)
Здесь и далее, говоря о точности моделирования временных рядов (аппроксимации, прогнозирования) будем применять значения показателей MAE (2.9) и MAPE (2.10).
В настоящем разделе была рассмотрена аппроксимация одной выборки временного ряда при помощи другой, лежащей на оси времени на отчетов левее, то есть раньше. Данное свойство представления новых выборок временного ряда при помощи старых будет использовано для определения модели экстраполяции.
2.1.3. Подобие выборок
Свойство двух выборок, заключенное в том, что одна выборка может быть выражена через другую с помощью линейной зависимости (2.1), назовем подобием двух выборок.
Покажем, что для общего случая линейной регрессии минимум ошибки регрессии соответствует максимуму линейной корреляции Пирсона. Пусть дана модель
Тогда функция суммы квадратов определяется как разность модельных 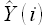 и фактических значений Y(i) некоторых наблюдений [19]
и фактических значений Y(i) некоторых наблюдений [19]
Обозначим 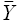 — среднее значение модельных и фактических наблюдений, которые по свойству линейной регрессии равны
— среднее значение модельных и фактических наблюдений, которые по свойству линейной регрессии равны
Из книги [19] известно, что сумма квадратов отклонений исследуемых наблюдений Y(i) от среднего значения 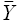 складывается из суммы квадратов отклонений модельных значений
складывается из суммы квадратов отклонений модельных значений 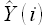 от
от 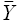 и суммы квадратов ошибок регрессии, определенной в выражении (2.12). Таким образом имеет место соотношение
и суммы квадратов ошибок регрессии, определенной в выражении (2.12). Таким образом имеет место соотношение
Выразим ошибку регрессии 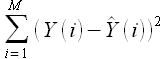 и получим
и получим
Величина
называется квадратом множественного коэффициента корреляции. Иногда данный коэффициент называются коэффициентом детерминации.
Стоит обратить внимание на то, что при Y(i) = const для i = {1,2,3,...} знаменатель R2 обращается в ноль. Однако по свойству регрессии [19], для такого случая модельные значения также будут постоянными 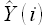 (i) = const для i = {1,2,3,...} и R2 = 1. Известно, что на практике такой случай невозможен, в связи с тем, что значения Y(i), как правило, являются результатами измерений.
(i) = const для i = {1,2,3,...} и R2 = 1. Известно, что на практике такой случай невозможен, в связи с тем, что значения Y(i), как правило, являются результатами измерений.
Преобразовав (2.15) получим выражение
При этом сумма квадратов отклонений исследуемых наблюдений Y(i) от среднего значения 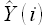 является величиной неизменной и характеризует свойство наблюдаемого процесса. Таким образом, из равенства (2.17) очевидно, что при
является величиной неизменной и характеризует свойство наблюдаемого процесса. Таким образом, из равенства (2.17) очевидно, что при 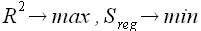 .
.
Далее рассмотрим коэффициент линейной корреляции Пирсона ρ, определяемый выражением
Согласно анализу, представленному в книге [19], связь двух рассматриваемых коэффициентов имеет следующий вид
Таким образом, известно, что модуль величины ρ(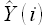 , Y) равен модулю величины R, а, следовательно, можно сформулировать следующее свойство
, Y) равен модулю величины R, а, следовательно, можно сформулировать следующее свойство
Все подробности регрессионного анализа, а также связи рассматриваемых коэффициентов приведены в книге [19].
Вернемся к исследуемым выборкам временного ряда. Пусть дан временной ряд 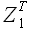 , для некоторой выборки
, для некоторой выборки 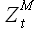 , принадлежащей данному временному ряду, определим все значения
, принадлежащей данному временному ряду, определим все значения 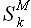 (α1,α0) для k = {1,2,...,t-1}, M = const. Далее, в множестве значений найдем минимальное
(α1,α0) для k = {1,2,...,t-1}, M = const. Далее, в множестве значений найдем минимальное
Согласно свойству (2.20) минимум ошибки регрессии 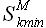 соответствует максимуму модуля коэффициента линейной корреляции (2.18). То есть если для k = {1,2,...,t-1} и M = const определить множество значений модуля корреляции
соответствует максимуму модуля коэффициента линейной корреляции (2.18). То есть если для k = {1,2,...,t-1} и M = const определить множество значений модуля корреляции
а после определить максимальное значение полученного множества
то задержка kmin из выражения (2.21) и задержка kmax из выражения (2.23) будут равны между собой, т. е. kmin = kmax. Проведенные расчеты подтверждают данное утверждение.
Определенную в (2.21) и (2.23) задержку, соответствующую минимуму ошибки регрессии 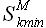 и максимуму модуля корреляции
и максимуму модуля корреляции 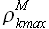 обозначим , а выборку
обозначим , а выборку 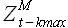 назовем выборкой максимального подобия (most similar pattern). Выборка максимального подобия
назовем выборкой максимального подобия (most similar pattern). Выборка максимального подобия 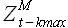 является выборкой, которая при подстановке в уравнение (2.2), дает в результате значения выборки
является выборкой, которая при подстановке в уравнение (2.2), дает в результате значения выборки 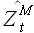 , которая максимально точно описывает исходную выборку
, которая максимально точно описывает исходную выборку 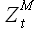 .
.
При реализации вычислений для определения выборки максимального подобия 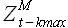 можно использовать как значения ошибки
можно использовать как значения ошибки 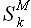 , так и значения модуля корреляции
, так и значения модуля корреляции 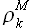 . В приведенном в диссертации примере использовалось значение коэффициента линейной корреляции (раздел 3.1.).
. В приведенном в диссертации примере использовалось значение коэффициента линейной корреляции (раздел 3.1.).
Гипотеза подобия. Если исходная выборка 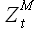 и модельная выборка
и модельная выборка 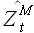 , полученная на основании (2.2) с использованием выборки
, полученная на основании (2.2) с использованием выборки 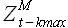 , имеют значение величины
, имеют значение величины 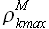 , близкое к единице, то для некоторых значений P и выборок
, близкое к единице, то для некоторых значений P и выборок 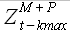 ,
, 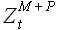 значение величины
значение величины 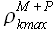 также близко к единице.
также близко к единице.
Аналогичным образом можно сформулировать гипотезу подобия в случае учета ошибок регрессии 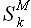 : если исходная выборка
: если исходная выборка 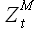 и модельная выборка
и модельная выборка 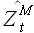 , полученная по формуле (2.2) на основании выборки
, полученная по формуле (2.2) на основании выборки 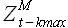 , имеют минимальное значение ошибки
, имеют минимальное значение ошибки 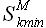 , то для некоторых значений P и выборок
, то для некоторых значений P и выборок 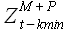 ,
, 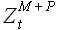 значение величины ошибки регрессии
значение величины ошибки регрессии  . Далее в работе использована первая формулировка гипотезы подобия.
. Далее в работе использована первая формулировка гипотезы подобия.
Представленные в четвертой главе диссертации результаты прогнозирования подтверждают справедливость гипотезы для исследуемых временных рядов. Для временных рядов из других предметных областей справедливость гипотезы необходимо проверять.
2.1.4. Описание модели экстраполяции
Пусть дан временной ряд 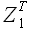 . Для данного временного ряда требуется определить значения
. Для данного временного ряда требуется определить значения 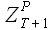 . Используя свойство выборок, сформулированное в разделе 2.1.3., выразим выборку
. Используя свойство выборок, сформулированное в разделе 2.1.3., выразим выборку 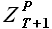 через некоторую выборку
через некоторую выборку 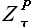 , лежащую внутри исходного временного ряда
, лежащую внутри исходного временного ряда 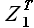
Алгоритм определения выборки 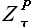 состоит из двух шагов.
состоит из двух шагов.
1. Определение выборки 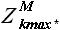 .
.
2. Вычисление 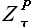 .
.
Рассмотрим подробно каждый шаг.
Определение выборки 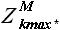 . На данном шаге для выборки
. На данном шаге для выборки 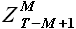 , содержащей значения процесса непосредственно перед моментом прогноза, находим выборку максимального подобия
, содержащей значения процесса непосредственно перед моментом прогноза, находим выборку максимального подобия 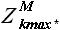 . Поиск выборки максимального подобия осуществляем перебором всех возможных значений задержек k = {1,2,...,T-M-1}. Для каждого значения k из указанного диапазона решаем задачу аппроксимации (раздел 2.1.2.), в результате которой определяем коэффициенты α1 и α0, соответствующие k. Далее для найденной пары коэффициентов определяем значение модельной выборки
. Поиск выборки максимального подобия осуществляем перебором всех возможных значений задержек k = {1,2,...,T-M-1}. Для каждого значения k из указанного диапазона решаем задачу аппроксимации (раздел 2.1.2.), в результате которой определяем коэффициенты α1 и α0, соответствующие k. Далее для найденной пары коэффициентов определяем значение модельной выборки 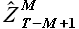 , на основании которых вычисляем значение (2.22). После того, как множество значений
, на основании которых вычисляем значение (2.22). После того, как множество значений 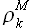 для k = {1,2,...,T-M-1} получено, определяем значение
для k = {1,2,...,T-M-1} получено, определяем значение 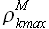 по выражению (2.23) и соответствующую выборку
по выражению (2.23) и соответствующую выборку 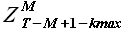 . Для упрощения обозначим задержку kmax* = T-M+1-kmax и выборку максимального подобия
. Для упрощения обозначим задержку kmax* = T-M+1-kmax и выборку максимального подобия 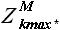 (SimilarHistory).
(SimilarHistory).
Вычисление 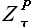 . В соответствии с гипотезой подобия, сформулированной в (разделе 2.1.3.), в качестве выборки
. В соответствии с гипотезой подобия, сформулированной в (разделе 2.1.3.), в качестве выборки 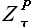 используем выборку
используем выборку 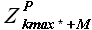 , то есть выборку, расположенную на оси времени сразу за выборкой максимального подобия. Выборку
, то есть выборку, расположенную на оси времени сразу за выборкой максимального подобия. Выборку 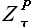 назовем базовой историей (BaseHistory). На рисунке 2.6 представлено расположение всех рассмотренных выборок.
назовем базовой историей (BaseHistory). На рисунке 2.6 представлено расположение всех рассмотренных выборок.
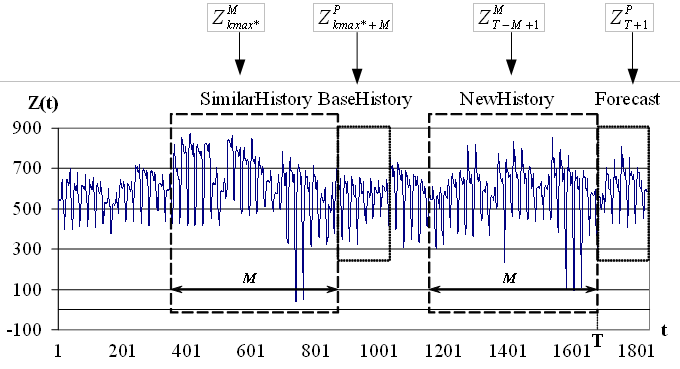
Рис. 2.6. Положение выборок на оси времени
Экстраполированные значения выборки 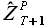 (прогноз, Forecast) определяются по формуле
(прогноз, Forecast) определяются по формуле
которая представляет собой модель экстраполяции временных рядов по выборке максимального подобия (extrapolation model on most similar pattern, далее EMMSP). В работе [40] используется термин closest pattern, в работе [42] — closest piece, в работе [41] — most similar vector.
Особенности EMMSP:
- модель относится к классу авторегрессионных моделей прогнозирования;
- модель может работать с неравноотстоящими временными рядами;
- модель работает со стационарными и нестационарными временными рядами;
- модель имеет один параметр M, определение которого подробно рассмотрено в третьей главе диссертации;
- экстраполяция P значений временного ряда производится за одну итерацию.
2.2. Модель с учетом внешних факторов
2.2.1 Выборки временных рядов
Пусть дан временной ряд Z(t) и внешние факторы, представленные в виде временных рядов X1(t),…,XS(t), соответствующие исходному ряду по отметкам времени. Требуется построить модель прогнозирования исходного временного ряда Z(t), которая будет учитывать влияние значений внешних факторов X1(t),…,XS(t).
Если внешние факторы X1(t),…,XS(t) имеют временное разрешение, отличное от разрешения исходного ряда Z(t), то необходимо произвести дополнительные преобразования и привести внешние факторы в соответствие с исходным временном рядом Z(t) по отметкам времени.
В основу модели экстраполяции с учетом внешнего фактора положено предположение о повторяемости выборок временного ряда (2.1.1.). Кроме того, известно, что для учета внешних факторов в авторегрессионных моделях вводятся дополнительные регрессоры (раздел 1.3.2.).
В настоящем разделе сначала рассматривается задача аппроксимации одной выборки при помощи другой с учетом выборок внешних факторов, а затем результаты аппроксимации применяются для построения модели прогнозирования временного ряда.
2.2.2 Аппроксимация выборки
Пусть задана выборка исходного временного ряда 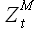 и выборки
и выборки 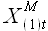 ,...,
,...,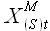 являются выборками внешних факторов, соответствующих
являются выборками внешних факторов, соответствующих 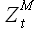 по отметкам времени. Аппроксимируем выборку
по отметкам времени. Аппроксимируем выборку 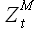 с учетом выборок
с учетом выборок 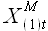 ,...,
,...,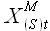 по формуле
по формуле
Здесь αS+1,αS,...,α0 — коэффициенты, определяемые по методу наименьших квадратов. Вектор EM — вектор значений ошибок аппроксимации, IM — единичный вектор. Выражение (2.26) можно переписать в виде
Постановка задачи аппроксимации выборки. Пусть дана функциональная зависимость (2.27). Необходимо определить такие значения коэффициентов αS+1,αS,...,α0, чтобы квадрат отклонений модельных значений выборки 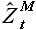 от фактических
от фактических 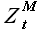 был минимален
был минимален
После нахождения коэффициентов αS+1,αS,...,α0, необходимо оценить вектор ошибок EM.
Решение. Пусть дана функциональная зависимость (2.26), тогда функция суммы квадратов имеет вид
Повторяя рассуждения, приведенные в разделе 2.1.2., приведем задачу к матричному уравнению
Решая матричное уравнение (2.30), определяем значения коэффициентов αS+1,αS,...,α0, соответствующие минимуму функции 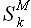 . Решение, как и в предыдущем случае, будет найдено при помощи обратной матрицы
. Решение, как и в предыдущем случае, будет найдено при помощи обратной матрицы
Оценка вектора ошибок аппроксимации EM описана в разделе 2.1.2.
2.2.3 Подобие выборок
Пусть дана выборка исходного временного ряда 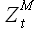 и выборки внешних факторов
и выборки внешних факторов 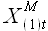 ,...,
,...,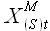 . Модельная выборка
. Модельная выборка 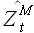 определяется линейной зависимостью (2.27). Вычислим все значения
определяется линейной зависимостью (2.27). Вычислим все значения 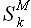 (αS+1,αS,...,α0) для задержек k = {1,2,...,t-1} и M = const. Далее, в множестве значений
(αS+1,αS,...,α0) для задержек k = {1,2,...,t-1} и M = const. Далее, в множестве значений 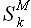 найдем минимальное по выражению (2.21). В случае множественной регрессии (2.27) равенство минимума ошибки регрессии (2.21) и максимума модуля линейной корреляции (2.23) не выполняется, а потому в данном случае следует рассматривать только ошибку регрессии
найдем минимальное по выражению (2.21). В случае множественной регрессии (2.27) равенство минимума ошибки регрессии (2.21) и максимума модуля линейной корреляции (2.23) не выполняется, а потому в данном случае следует рассматривать только ошибку регрессии 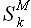 (αS+1,αS,...,α0).
(αS+1,αS,...,α0).
Определенную в выражении (2.21) задержку, соответствующую минимуму ошибки регрессии 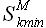 обозначим по аналогии с предыдущим случаем kmax, а выборку
обозначим по аналогии с предыдущим случаем kmax, а выборку 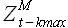 назовем выборкой максимального подобия (most similar pattern). Выборка максимального подобия
назовем выборкой максимального подобия (most similar pattern). Выборка максимального подобия 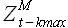 является выборкой, которая при подстановке в уравнение (2.27), дает в результате значения выборки
является выборкой, которая при подстановке в уравнение (2.27), дает в результате значения выборки 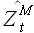 , которая максимально точно описывает исходную выборку
, которая максимально точно описывает исходную выборку 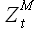 с учетом выборок внешних факторов
с учетом выборок внешних факторов 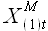 ,...,
,...,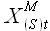 . Величину минимальной ошибки
. Величину минимальной ошибки 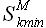 , соответствующую задержке kmax будем далее обозначать
, соответствующую задержке kmax будем далее обозначать 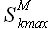 .
.
Гипотеза подобия. Если исходная выборка 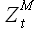 и модельная выборка
и модельная выборка 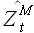 , полученная на основании (2.27) с использованием выборки
, полученная на основании (2.27) с использованием выборки 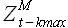 и выборок внешних факторов
и выборок внешних факторов 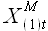 ,...,
,...,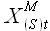 , имеют минимальное значение величины
, имеют минимальное значение величины 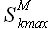 , то для некоторых значений P и выборок
, то для некоторых значений P и выборок 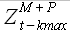 ,
,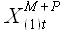 ,...,
,..., ,
,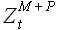 значение величины
значение величины 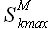 также стремится к минимальному.
также стремится к минимальному.
Представленные в четвертой главе диссертации результаты прогнозирования подтверждают справедливость гипотезы для исследуемых временных рядов. Для временных рядов из других предметных областей справедливость гипотезы необходимо проверять дополнительно.
2.2.4 Описание модели
Пусть дан исходный временной ряд 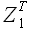 и внешние факторы
и внешние факторы 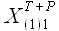 ,...,
,...,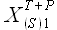 . Для исходного временного ряда требуется определить значения
. Для исходного временного ряда требуется определить значения 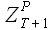 , учитывая доступные значения
, учитывая доступные значения 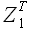 и
и 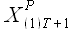 ,...,
,...,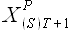 . Используя свойство выборок, сформулированное в разделе 2.2.3., выразим выборку
. Используя свойство выборок, сформулированное в разделе 2.2.3., выразим выборку 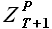 через некоторую выборку
через некоторую выборку 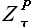 , лежащую внутри исходного временного ряда
, лежащую внутри исходного временного ряда 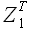 , и выборки
, и выборки 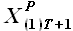 ,...,
,...,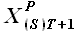 следующим образом
следующим образом
Алгоритм определения выборки 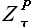 состоит из двух шагов.
состоит из двух шагов.
1. Определение выборки 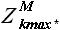 .
.
2. Вычисление 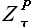 .
.
Определение выборки 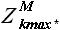 . На данном шаге, как в случае экстраполяции без учета внешних факторов, для выборки
. На данном шаге, как в случае экстраполяции без учета внешних факторов, для выборки 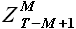 , содержащей значения процесса непосредственно перед моментом прогноза, находим выборку максимального подобия
, содержащей значения процесса непосредственно перед моментом прогноза, находим выборку максимального подобия 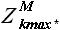 . Поиск выборки максимального подобия осуществляем перебором всех возможных значений задержек k = {1,2,...,T-M-1}. Для каждого значения k из указанного диапазона решаем задачу аппроксимации (2.2.2.), в результате которой определяем коэффициенты αS+1,αS,...,α0, соответствующие k. Далее для вычисленных коэффициентов определяем значение модельной выборки, на основании которых вычисляем значение ошибки регрессии
. Поиск выборки максимального подобия осуществляем перебором всех возможных значений задержек k = {1,2,...,T-M-1}. Для каждого значения k из указанного диапазона решаем задачу аппроксимации (2.2.2.), в результате которой определяем коэффициенты αS+1,αS,...,α0, соответствующие k. Далее для вычисленных коэффициентов определяем значение модельной выборки, на основании которых вычисляем значение ошибки регрессии 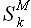 (2.22). После того, как множество значений
(2.22). После того, как множество значений 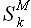 для k = {1,2,...,T-M-1} получено, определяем значение
для k = {1,2,...,T-M-1} получено, определяем значение 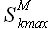 (2.23) и соответствующую выборку
(2.23) и соответствующую выборку 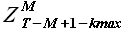 . Как и ранее обозначим задержку kmax* = T-M+1-kmax, а выборку максимального подобия
. Как и ранее обозначим задержку kmax* = T-M+1-kmax, а выборку максимального подобия 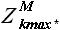 (SimilarHistory).
(SimilarHistory).
Вычисление 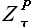 . В соответствии с гипотезой подобия, сформулированной в разделе 2.2.3., в качестве выборки
. В соответствии с гипотезой подобия, сформулированной в разделе 2.2.3., в качестве выборки 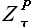 в выражении (2.33) используем выборку
в выражении (2.33) используем выборку 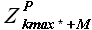 , то есть выборку, расположенную на оси времени сразу за выборкой максимального подобия. Для случая учета одного внешнего фактора положение выборок показано на рисунке 2.7.
, то есть выборку, расположенную на оси времени сразу за выборкой максимального подобия. Для случая учета одного внешнего фактора положение выборок показано на рисунке 2.7.
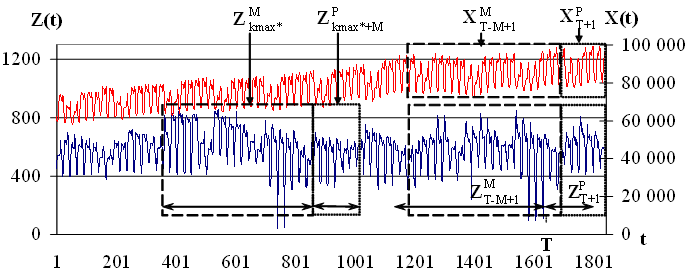
Рис. 2.7. Положение выборок на оси времени
Для удобства назовем выборки следующим образом:
- выборка новой истории
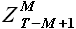 (NewHistory);
(NewHistory); - выборка максимального подобия
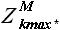 (SimilarHistory);
(SimilarHistory); - выборка базовой истории
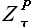 (BaseHistory);
(BaseHistory); - выборка истории внешнего фактора
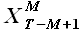 (FactorHistory);
(FactorHistory); - выборка прогноза внешнего фактора
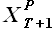 (FactorForecast).
(FactorForecast).
Экстраполированные значения выборки 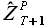 (Forecast) определяем по формуле
(Forecast) определяем по формуле
которая представляет собой расширенную модель экстраполяции временных рядов по выборке максимального подобия (extrapolation model on most similar pattern extended, далее EMMSPX).
Необходимо заметить, что внешние факторы, как правило, оказывают влияние на исследуемый процесс в соответствующий момент времени. Например, из работы [9] известно, что на энергопотребление оказывает существенное влияние температура окружающей среды, а именно: при резких изменениях температуры скачкообразно меняется энергопотребление (рис. 2.8). Таким образом, по свойству процессов учет внешних факторов необходим в соответствующий момент времени. В случае, если отсутствуют значения внешних факторов на будущий период, а именно, значения выборок 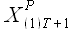 ,...,
,...,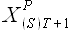 , то необходимо или спрогнозировать прежде внешние факторы, а потом исследуемый основной процесс, либо удалить внешние факторы из модели. В случае прогноза энергопотребления часто в качестве внешнего фактора используется прогноз температуры окружающей среды, формируемый Гидрометцентром России.
, то необходимо или спрогнозировать прежде внешние факторы, а потом исследуемый основной процесс, либо удалить внешние факторы из модели. В случае прогноза энергопотребления часто в качестве внешнего фактора используется прогноз температуры окружающей среды, формируемый Гидрометцентром России.
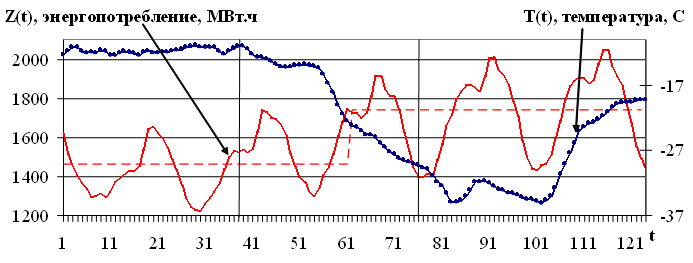
Рис. 2.8. Влияние температуры окружающей среды на энергопотребление Новосибирской области
На рисунке 2.8 представлены графики энергопотребления Новосибирской области, а также температура окружающей среды той же территории. Заметно, что резкое снижение температуры приводит к скачкообразному повышению энергопотребления. Таким образом, по свойству данных процессов учет температуры при прогнозе энергопотребления должен производиться в соответствующие моменты времени.
В завершении данного раздела необходимо отметить особенности EMMSPX:
- модель относится к классу авторегрессионных моделей прогнозирования, учитывающих дискретные внешние факторы;
- модель может учитывать несколько дискретных внешних факторов;
- модель эффективно работает с неравноотстоящими временными рядами;
- модель работает со стационарными и нестационарными временными рядами;
- модель имеет один параметр M, определение которого подробно рассмотрено в третьей главе диссертации;
- экстраполяция P значений временного ряда производится за одну итерацию.
2.3. Варианты моделей по выборке максимального подобия
Модель (2.34) можно разделить на две части — модель авторегрессии и модель внешнего фактора
Модель авторегрессии и модель внешнего фактора могут быть модифицированы с целью повышения точности прогнозирования.
Авторегрессионная EMMSP со множеством выборок. Прогнозные значения 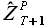 вычисляются как линейная комбинация нескольких выборок базовой истории с различными задержками
вычисляются как линейная комбинация нескольких выборок базовой истории с различными задержками
В рамках диссертации проводились исследования эффективности увеличения количества выборок, принимаемых в расчет. На практике количество используемых выборок исходного временного ряда не превышает двух, т. е. прогнозные значения 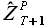 вычисляются как линейная комбинация двух выборок базовой истории с различными задержками
вычисляются как линейная комбинация двух выборок базовой истории с различными задержками
Однако не исключено, то в ряде задач полезным будет использование трех-четырех выборок. Данная модель (2.37) применялась для прогнозирования временных рядов цен на электроэнергию [45].
Авторегрессионная EMMSP с использованием q-той степени значений выборок. Модель прогнозирования представляет собой линейную комбинацию степеней выборки максимального подобия
Здесь 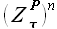 — выборка, значениями которой являются -ные степени значений временного ряда
— выборка, значениями которой являются -ные степени значений временного ряда
В рамках диссертации проводились исследования эффективности повышения степени выборки максимального подобия, которые показали, что точность прогнозирования для некоторых временных рядов повышается при использовании второй степени, то есть модели
Дальнейшее увеличение степени выборки максимального подобия эффективности модели не повышает.
EMMSPX с использованием q-той степени значений внешних факторов. В случае доступности данных лишь по одному внешнему фактору возможна модификация модели аналогично (2.38)
При этом значения выборки определяются как -ные степени значений внешнего фактора (2.39).
Важно отметить, что при построении моделей (2.36) — (2.41) применяется единообразный подход к анализу и проектированию моделей, описанный в разделе 2.2. настоящей работы.
Ограничения применимости модели экстраполяции временных рядов по выборке максимального подобия. Предложенные в настоящей главе модели EMMSP и EMMSPX могут применяться для прогнозирования временных рядов на значений вперед при выполнении набора условий.
- Длина временного ряда составляет не менее 500 P - 700 P.
- Временной ряд равноотстоящий; в случае неравноотстоящего временного ряда применение модели возможно только при условии, что его равноотстоящие отрезки должны быть содержать не менее, чем 100 P - 150 P отсчетов.
- Временной ряд относится к классу временных рядов с длинной памятью.
- Задача прогнозирования на P значений вперед относится к классу краткосрочного или среднесрочного прогнозирования данного типа временного ряда. Не рекомендуется использовать разработанную модель для долгосрочного прогнозирования.
- В случае учета набора дискретных внешних факторов, их временное разрешение должно быть приведено к разрешению исходного временного ряда. Длина исходного временного ряда и временных рядов внешних факторов может не совпадать.
2.4. Выводы
1) В настоящей главе предложены модели экстраполяции временных рядов по выборке максимального подобия с учетом и без учета внешних факторов.
2) Предложенные модели относятся к классу авторегрессионных моделей прогнозирования и обладают всеми достоинствами, характерными для данного класса.
3) Предложенные модели устраняют существенный недостаток указанного класса — большое число свободных параметров, требующих идентификации. Обе модели экстраполяции по выборке максимального подобия имеют единственный параметр.
4) Разработаны варианты моделей по выборке максимального подобия, использование которых может приводить к повышению точности прогнозирования временного ряда.
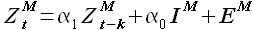 (2.1)
(2.1)
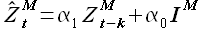 (2.2)
(2.2)
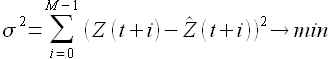 (2.3)
(2.3)
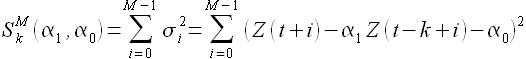 (2.4)
(2.4)
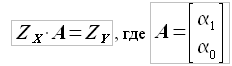 (2.5)
(2.5)
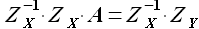 (2.6)
(2.6)
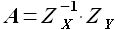 (2.7)
(2.7)
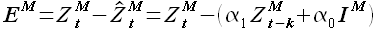 (2.8)
(2.8)
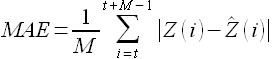 (2.9)
(2.9)
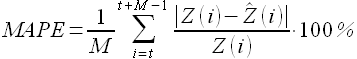 (2.10)
(2.10)
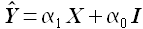 (2.11)
(2.11)
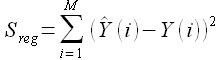 (2.12)
(2.12)
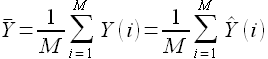 (2.13)
(2.13)
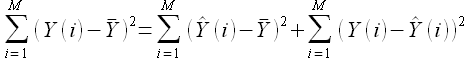 (2.14)
(2.14)
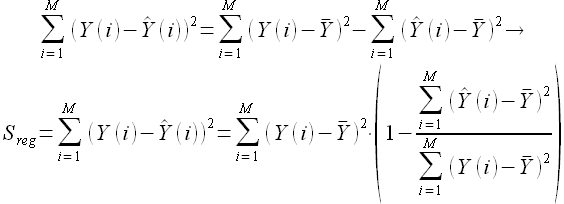 (2.15)
(2.15)
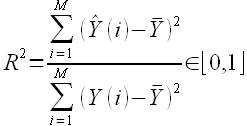 (2.16)
(2.16)
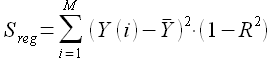 (2.17)
(2.17)
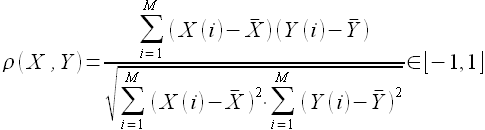 (2.18)
(2.18)
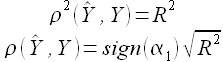 (2.19)
(2.19)
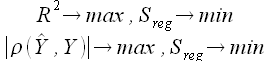 (2.20)
(2.20)
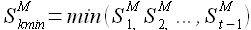 (2.21)
(2.21)
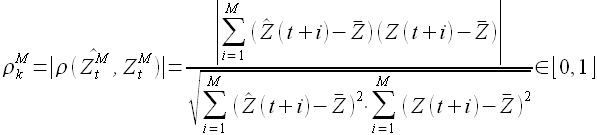 (2.22)
(2.22)
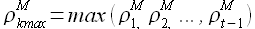 (2.23)
(2.23)
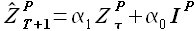 (2.24)
(2.24)
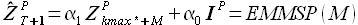 (2.25)
(2.25)
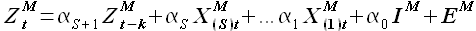 (2.26)
(2.26)
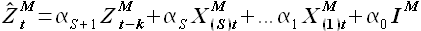 (2.27)
(2.27)
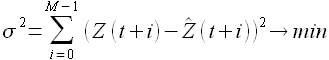 (2.28)
(2.28)
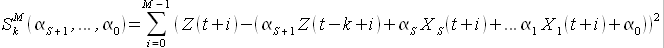 (2.29)
(2.29)
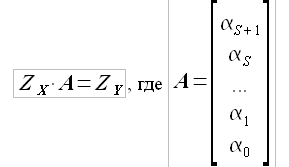 (2.30)
(2.30)
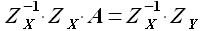 (2.31)
(2.31)
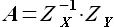 (2.32)
(2.32)
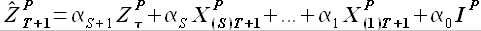 (2.33)
(2.33)
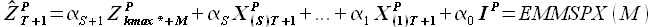 (2.34)
(2.34)
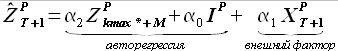 (2.35)
(2.35)
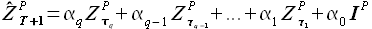 (2.36)
(2.36)
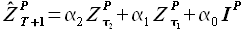 (2.37)
(2.37)
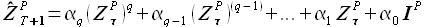 (2.38)
(2.38)
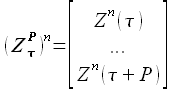 (2.39)
(2.39)
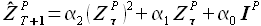 (2.40)
(2.40)
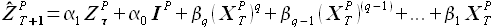 (2.41)
(2.41)