Постановка задачи и исходные данные

Исторические данные содержали месячные объемы продаж чуть более чем за 3 года - всего 41 значение по 5 временным рядам техники различных видов:

• встраиваемая техника
• крупная бытовая техника (холодильники, стиральные машины и т.д.)
• компьютеры
• мелкая бытовая техника
• теле видео аудио.

По предоставленным историческим данным требовалось построить прогноз на 3 месяца вперед для каждого временного ряда.

Важно отметить, что поставленная задача прогнозирования относится к классу долгосрочного прогнозирования. Долгосрочный прогноз не вычисляется автоматически. Как он формируется? Обычно используют нехитрые математические модели, а далее полученный на них результат оценивает эксперт, который владеет искомой предметной областью и знает все ее нюансы. То есть расчет модели прогнозирования является основой для работы эксперта. Внутри этой задачи практически нет места для автоматизации.

Модели прогнозирования

Говоря о математических моделях для долгосрочного прогноза, нужно сказать, что наиболее популярной моделью прогнозирования является экспоненциальное сглаживание. Отчего? Оттого, что данная модель умеет весьма гибко работать с небольшими объемами исходных значений. Если мы говорим о моделях прогнозирования вообще, то здесь, безусловно, наиболее популярными являются модели ARIMAX (авторегрессия) и ANN (нейронные сети). Однако это большие и сложные модели, для которых нужны сотни и тысячи фактических значений, чтобы построить такую модель, а потом использовать ее для прогнозирования. Нельзя построить надежную модель ARIMAX на нескольких десятках исходных значений временного ряда; нельзя и нейронную сеть обучить на таком количестве исходных значений.

Экспоненциальное сглаживание

Модель экспоненциального сглаживания была разработана давно, еще в середине XX века, однако с тех пор не потеряла своей актуальности и эффективности, если речь идет и долгосрочном прогнозировании на малом объеме исходных данных. В диссертации есть раздел с описанием экспоненциального сглаживания, однако не смущайтесь громоздкости формул — идея модели чрезвычайно проста! Из литературы могу посоветовать отличную статью Prajakta S.K. «Time series Forecasting using Holt-Winters Exponential Smoothing», на основании которой можно программно реализовать алгоритмы экспоненциального сглаживания.

Суть модели заключается в следующем

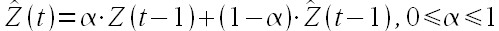
т. е. будущее значение временного ряда есть взвешенное среднее от предыдущего значения временного ряда и предыдущего прогноза. Если установить α = 0.5, то мы получим простую формулу для вычисления будущего значения

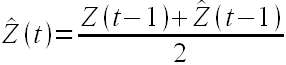
Можно немного модифицировать предложенный подход и положить в основу модели прогнозирования другую зависимость

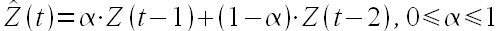
т.е. будущее значение временного ряда является взвешенным средним его двух предыдущих значений.

Если у нас есть во временном ряде сезонность, например годовая для месячного ряда, то можно попробовать применить модель Хольта-Винтерса — одну из модификаций экспоненциального сглаживания (подробности описаны в указанной статье), а можно упростить до выражения

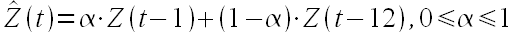
т.е. определять будущее значение ряда как взвешенное среднее от предыдущего значения и значения за прогнозный месяц прошлого года.

Такого рода модификаций можно сделать массу. Например, если нам нужно взвесить не два, а три значения, то удобно использовать следующий подход

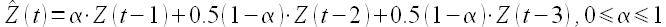
т.е. определять взвешенное среднее трех значений временного ряда с использованием единственного параметра α. Аналогичным образом можно взвешивать значения с учетом сезонности

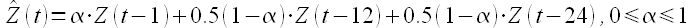
Как определить значение параметра α?

На параметр α в модели имеется жесткое ограничение — [0,1], так что его удобнее всего определять простым перебором значений, например, с шагом 0.1. Таким образом для 10 значений α нужно посчитать прогноз по имеющимся данным и сравнить его с фактом. То значение α, для которого прогноз будет максимально точным, можно считать окончательным параметром модели.

Резюме

Надо ясно понимать, что математика наука полезная, но не всесильная. Если у нас с вами на входе в расчеты всего 40 значений, а характер временного ряда весьма сложный, то сделать точную и адекватную математическую модель прогнозирования для такого временного ряда почти невозможно. Наиболее адекватной моделью, которую стоит опробовать в первую очередь, является экспоненциальное сглаживание и его модификации.

Как правило такого рода прогнозы делают эксперты предметной области, которые годами работают в данной сфере и понимают тонкости не математики, а в первую очередь продаж, тенденций, рынков и т.д. Математика в их руках лишь инструмент, который им дает статистические оценки данных, но окончательное значение формируют они. Если перед вами стоит задача вычислять такой прогноз, то настоятельно рекомендую обратиться к статье Пять способов повысить точность прогнозов.

Во второй части своей записи об этом случае я покажу, в чем состоят узкие места применения экспоненциального сглаживания для такого прогнозирования и почему в обязательном порядке требуется производить экспертную оценку полученных прогнозных значений.