В предыдущей записи я подняла тему популярной модели прогнозирования временных рядов ARIMAX и рассмотрела авторегрессию. В настоящей заметке рассмотрю подробнее интеграцию (integrated).

Когда нам нужно прогнозировать временной ряд 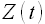, то иногда удобнее и точнее прогнозировать не само значение процесса 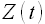, а только его изменение. То есть на первом этапе мы из исходного временного ряда 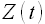получаем временной ряд 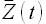, который является разностью соседних значений:

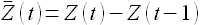
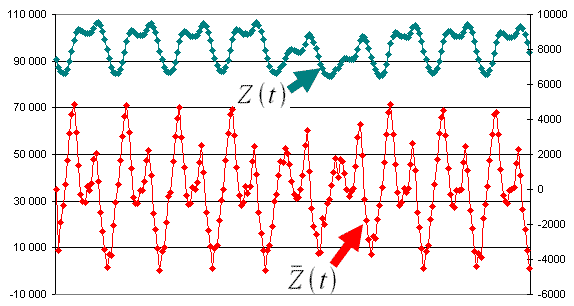
Ниже на графике представлен сначала исходный временной ряд (зеленый), а далее разностный (красный), то есть полученный вычитанием соседних значений.

Далее, мы работаем уже с полученным рядом 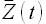и определяем будущее значение не 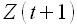, а 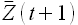с использованием уже рассмотренной модели авторегрессии.

Отчего такая операция называется integrated, то есть интегрированием? В действительности, приведенная разность является обратной операцией, однако при использовании такого подхода для получения в конечном итоге будущего значения искомого временного ряда 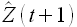необходимо будет суммировать 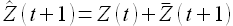, то есть к текущему значению процесса прибавлять спрогнозированную разность. Так как суммировать в итоге нужно единожды, то говорят об интеграции первого порядка.

Тонкости использования интеграции в модели ARIMAX

Во-первых, иногда на практике модель временного ряда получается адекватнее, если использовать интеграцию второго порядка, то есть делать не одно вычитание, а два последовательно:

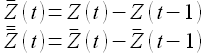
В таком случае интегрировать, то есть суммировать, придется дважды, чтобы спрогнозировать будущее значение искомого временного ряда 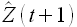. Обращаю внимание на то, что брать порядок интеграции больше 2 неразумно, так как давно показана неэффективность подобных моделей.

Во-вторых, если временной ряд имеет определенную периодичность, например, почасовые временные ряды часто имеют суточную периодичность, то можно получать разностный ряд 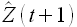с учетом такой периодичности, например, для временного ряда энергопотребления брать разность следующим образом:

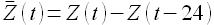
Вот таким вот образом определяется интеграция в модели прогнозирования временных рядов ARIMAX.