Скачать полный текст диссертации в формате PDF (2.9 Мб).
Глава 1. Постановка задачи и обзор моделей прогнозирования временных рядов
Глава 1. Постановка задачи и обзор моделей прогнозирования временных рядов
1.1. Содержательная постановка задачи
1.2. Формальная постановка задачи
1.3. Обзор моделей прогнозирования
1.3.1. Регрессионные модели
1.3.2. Авторегрессионные модели
1.3.3. Модели экспоненциального сглаживания
1.3.4. Нейросетевые модели
1.3.5. Модели на базе цепей Маркова
1.3.6. Модели на базе классификационно-регрессионных деревьев
1.3.7. Другие модели и методы прогнозирования
1.4. Сравнение моделей прогнозирования
1.4.1. Достоинства и недостатки моделей
1.4.2. Комбинированные модели
1.5. Выводы
В текст диссертации включены вставки со ссылками на полезные записи блога, в которых я простым языком рассказываю о моделях прогнозирования и привожу примеры реализации.
— Нейронные сети рассмотрены в наборе записей по тэгу Нейронные сети.
— Модель ARIMAX подробно описана в четырех записях по тэгу ARIMAX.
— Описание и примеры реализации экспоненциального сглаживания приведены по тэгу Экспоненциальное сглаживание.
— Опубликованы записи по вопросам классификации моделей прогнозирования.
— Полный перечень материалов о моделях прогнозирования смотри по тэгу Модели прогнозирования.
1.1. Содержательная постановка задачи
Слово прогноз возникло от греческого 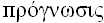 , что означает предвидение, предсказание. Под прогнозированием понимают предсказание будущего с помощью научных методов. Процессом прогнозирования называется специальное научное исследование конкретных перспектив развития какого-либо процесса. Согласно работе [1] процессы, перспективы которых необходимо предсказывать, чаще всего описываются временными рядами, то есть последовательностью значений некоторых величин, полученных в определенные моменты времени. Временной ряд включает в себя два обязательных элемента — отметку времени и значение показателя ряда, полученное тем или иным способом и соответствующее указанной отметке времени. Каждый временной ряд рассматривается как выборочная реализация из бесконечной популяции, генерируемой стохастическим процессом, на который оказывают влияние множество факторов [1]. На рисунке 1.1 представлен пример временного ряда цен на электроэнергию европейской территории РФ.
, что означает предвидение, предсказание. Под прогнозированием понимают предсказание будущего с помощью научных методов. Процессом прогнозирования называется специальное научное исследование конкретных перспектив развития какого-либо процесса. Согласно работе [1] процессы, перспективы которых необходимо предсказывать, чаще всего описываются временными рядами, то есть последовательностью значений некоторых величин, полученных в определенные моменты времени. Временной ряд включает в себя два обязательных элемента — отметку времени и значение показателя ряда, полученное тем или иным способом и соответствующее указанной отметке времени. Каждый временной ряд рассматривается как выборочная реализация из бесконечной популяции, генерируемой стохастическим процессом, на который оказывают влияние множество факторов [1]. На рисунке 1.1 представлен пример временного ряда цен на электроэнергию европейской территории РФ.
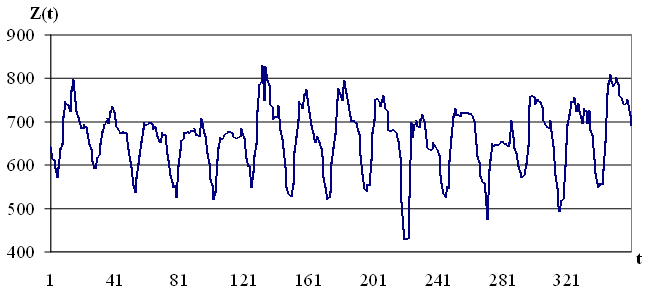
Рис. 1.1 Временной ряд цен на электроэнергию
Простым языком о видах временных рядов смотри запись блога Характеристики прогнозируемых временных рядов
Одна из классификаций временных рядов приведена в работе [6]. Согласно этой работе, временные ряды различаются способом определения значения, временным шагом, памятью и стационарностью.
- интервальные временные ряды,
- моментные временные ряды.
Интервальный временной ряд представляет собой последовательность, в которой уровень явления (значение временного ряда) относят к результату, накопленному или вновь произведенному за определенный интервал времени. Интервальным, например, является временной ряд показателя выпуска продукции предприятием за неделю, месяц или год; объем воды, сброшенной гидроэлектростанцией за час, день, месяц; объем электроэнергии, произведенной за час, день, месяц и другие.
Если же значение временного ряда характеризует изучаемое явление в конкретный момент времени, то совокупность таких значений образует моментный временной ряд. Примерами моментных рядов являются последовательности финансовых индексов, рыночных цен; физические показатели, такие как температура окружающего воздуха, влажность, давление, измеренные в конкретные моменты времени, и другие.
В зависимости от частоты определения значений временного ряда, они делятся на
- равноотстоящие временные ряды,
- неравноотстоящие временные ряды.
Равноотстоящие временные ряды формируются при исследовании и фиксации значений процесса в следующие друг за другом равные интервалы времени. Большинство физических процессов описываются при помощи равноотстоящих временных рядов. Неравноотстоящими временными рядами называются те ряды, для которых принцип равенства интервалов фиксации значений не выполняется. К таким рядам относятся, например, все биржевые индексы в связи с тем, что их значения определяются лишь в рабочие дни недели.
В зависимости от характера описываемого процесса временные ряды разделяются на
- временные ряды длинной памяти,
- временные ряды короткой памяти.
Задача отнесения временного ряда к рядам с короткой или длинной памятью описана в статье [7]. В целом, говоря о временных рядах с длинной памятью, подразумеваются временные ряды, для которых автокорреляционная функция, введенная в книге [1], убывает медленно. К временным рядам с короткой памятью относят временные ряды, автокорреляционная функция которых убывает быстро. Скорость потока транспорта по дорогам, а также многие физические процессы, такие как потребление электроэнергии, температура воздуха, относятся к временным рядам с длинной памятью [7]. К временным рядам с короткой памятью относятся, например, временные ряды биржевых индексов.
Дополнительно временные ряды принято разделять на
- стационарные временные ряды,
- нестационарные временные ряды.
Стационарным временным рядом называется такой ряд, который остается в равновесии относительно постоянного среднего уровня. Остальные временные ряды являются нестационарными. В книге [1] указано, что и в промышленности, и в торговле, и в экономике, где прогнозирование имеет важное значение, многие временные ряды являются нестационарными, то есть не имеющими естественного среднего значения. Нестационарные временные ряды для решения задачи прогнозирования часто приводятся к стационарным при помощи разностного оператора [1].
Горизонты прогнозирования рассмотрены также в записи блога Горизонты прогнозирования временных рядов
Горизонт времени, на который необходимо определить значения временного ряда, называется временем упреждения [1]. В зависимости от времени упреждения задачи прогнозирования, как правило, делятся на следующие категории срочности:
- долгосрочное прогнозирование;
- среднесрочное прогнозирование;
- краткосрочное прогнозирование.
Важно отметить, что для каждого временного ряда приведенная классификация имеет собственные диапазоны. Например, для временного ряда уровня сахара крови классификация срочности задачи прогнозирования обуславливается типами инсулина [8]:
- ультракраткосрочное прогнозирование: до 3 – 4 часа;
- краткосрочное прогнозирование: до 5 – 8 часов;
- среднесрочное прогнозирование: до 16 – 24 часов.
Для задачи прогнозирования энергопотребления классификация задач предложена в работе [9]:
- ультракраткосрочное прогнозирование: до одного дня;
- краткосрочное прогнозирование: от одного дня до недели;
- среднесрочное прогнозирование: от одной недели до года;
- долгосрочное прогнозирование: более чем на год вперед.
То есть для различных временных рядов, с различным временным разрешением классификация срочности задач прогнозирования индивидуальна.
Говоря о прогнозировании временных рядов, необходимо различить два взаимосвязанных понятия — метод прогнозирования и модель прогнозирования.
Метод прогнозирования представляет собой последовательность действий, которые нужно совершить для получения модели прогнозирования временного ряда.
Модель прогнозирования есть функциональное представление, адекватно описывающее временной ряд и являющееся основой для получения будущих значений процесса. Часто, говоря о моделях прогнозирования, используется термин модель экстраполяции [10].
Метод прогнозирования содержит последовательность действий, в результате выполнения которой определяется модель прогнозирования конкретного временного ряда. Кроме того, метод прогнозирования содержит действия по оценке качества прогнозных значений. Общий итеративный подход к построению модели прогнозирования состоит из следующий шагов [1].
Шаг 1. На первом шаге на основании предыдущего собственного или стороннего опыта выбирается общий класс моделей для прогнозирования временного ряда на заданный горизонт.
Шаг 2. Определенный общий класс моделей обширен. Для непосредственной подгонки к исходному временному ряду, развиваются грубые методы идентификации подклассов моделей. Такие методы идентификации используют качественные оценки временного ряда.
Шаг 3. После определения подкласса модели, необходимо оценить ее параметры, если модель содержит параметры, или структуру, если модель относится к категории структурных моделей (раздел 1.3.). На данном этапе обычно используется итеративные способы, когда производится оценка участка (или всего) временного ряда при различных значениях изменяемых величин. Как правило, данный шаг является наиболее трудоемким в связи с тем, что часто в расчет принимаются все доступные исторические значения временного ряда.
Шаг 4. Далее производится диагностическая проверка полученной модели прогнозирования. Чаще всего выбирается участок или несколько участков временного ряда, достаточных по длине для проверочного прогнозирования и последующей оценки точности прогноза. Выбранные для диагностики модели прогнозирования участки временного ряда называются контрольными участками (периодами).
Шаг 5. В случае если точность диагностического прогнозирования оказалась приемлемой для задач, в которых используются прогнозные значения, то модель готова к использованию. В случае если точность прогнозирования оказалось недостаточной для последующего использования прогнозных значений, то возможно итеративное повторение всех описанных выше шагов, начиная с первого.
Моделью прогнозирования временного ряда является функциональное представление, адекватно описывающее временной ряд.
При прогнозировании временных рядов возможны два варианта постановки задачи. В первом варианте для получения будущих значений исследуемого временного ряда используются доступные значения только этого ряда. Во втором варианте для получения прогнозных значений возможно использование не только фактических значений искомого ряда, но и значений набора внешних факторов, представленных в виде временных рядов. В общем случае временные ряды внешних факторов могут иметь разрешение по времени отличное от разрешения искомого временного ряда. Например, в работе [9] подробно обсуждаются внешние факторы, оказывающие влияние на временной ряд энергопотребления. К таким внешним факторам относят температуру окружающей среды, влажность воздуха, а также сезонность, т. е. час суток, день недели, месяц года. В общем случае внешние факторы могут быть дискретными, т. е. представленными временными рядами, например, температура воздуха; или категориальными, т. е. состоящими из подмножеств, например, в зависимости от веса тела человека можно отнести к трем категориям: «легкий», «средний», «тяжелый». Лишь некоторые модели прогнозирования позволяют учитывать категориальные внешние факторы, большинство моделей позволяют учитывать только дискретных (раздел 1.3.).
При прогнозировании временного ряда требуется определить функциональную зависимость, адекватно описывающую временной ряд, которая называется моделью прогнозирования. Цель создания модели прогнозирования состоит в получении такой модели, для которой среднее абсолютное отклонение истинного значения от прогнозируемого стремится к минимальному для заданного горизонта, который называется временем упреждения. После того, как модель прогнозирования временного ряда определена, требуется вычислить будущие значения временного ряда, а также их доверительный интервал.
1.2. Формальная постановка задачи
Прогнозирование без учета внешних факторов. Пусть значения временного ряда доступны в дискретные моменты времени t = 1,2,...,T. Обозначим временной ряд Z(t) = Z(1), Z(2),...,Z(T). В момент времени T необходимо определить значения процесса Z(t) в моменты времени T+1,...,T+P. Момент времени T называется моментом прогноза, а величина P — временем упреждения [1].
1) Для вычисления значений временного ряда в будущие моменты времени требуется определить функциональную зависимость, отражающую связь между прошлыми и будущими значениями этого ряда
Зависимость (1.1) называется моделью прогнозирования. Требуется создать такую модель прогнозирования, для которой среднее абсолютное отклонение истинного значения от прогнозируемого стремится к минимальному для заданного P
Выражение (1.1) можно переписать в виде
где 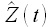 прогнозные (расчетные) значения временного ряда Z(t). Здесь и далее будем использовать «крышечку» для обозначения вычисляемых значений временного ряда.
прогнозные (расчетные) значения временного ряда Z(t). Здесь и далее будем использовать «крышечку» для обозначения вычисляемых значений временного ряда.
2) Кроме получения будущих значений  требуется определить доверительный интервал возможных отклонений этих значений.
требуется определить доверительный интервал возможных отклонений этих значений.
Задача прогнозирования временного ряда проиллюстрирована на рисунке 1.2.
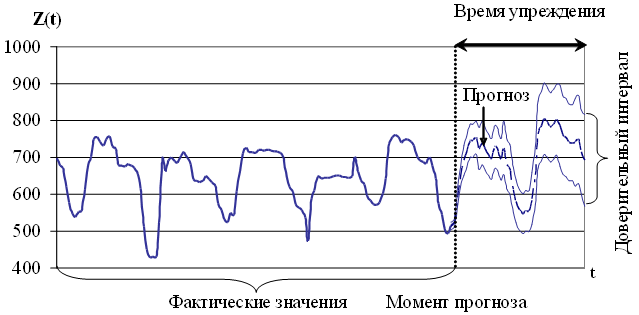
Рис. 1.2. Иллюстрация задачи прогнозирования временного ряда без учета внешних факторов
Прогнозирование с учетом внешних факторов. Пусть значения исходного временного ряда Z(t) доступны в дискретные моменты времени t = 1,2,...,T. Предполагается, что на значения Z(t) оказывает влияние набор внешних факторов. Пусть первый внешний фактор X1(t1) доступен в дискретные моменты времени t1 = 1,2,...,T1, второй внешний фактор X2(t2) доступен в моменты времени t2 = 1,2,...,T2 и т.д.
В случае, если дискретность исходного временного ряда и внешних факторов, а также значения T,T1,...,TS различны, то временные ряды внешних факторов X1(t1),...,XS(tS) необходимо привести к единой шкале времени t.
В момент прогноза T необходимо определить будущие значения исходного процесса Z(t) в моменты времени T+1,...,T+P, учитывая влияние внешних факторов X1(t),...,XS(t). При этом считаем, что значения внешних факторов в моменты времени X1(T+1),...,X1(T+P),...,XS(T+1),...,XS(T+P) являются доступными.
1) Для вычисления будущих значений процесса Z(t) в указанные моменты времени требуется определить функциональную зависимость, отражающую связь между прошлыми значениями Z(t) и будущими, а также принимающую во внимание влияние внешних факторов X1(t),...,XS(t) на исходный временной ряд
Зависимость (1.4) называется моделью прогнозирования с учетом внешних факторов X1(t),...,XS(t). Требуется создать такую модель прогнозирования, для которой среднее абсолютное отклонение истинного значения от прогнозируемого стремится к минимальному для заданного P (1.2).
2) Кроме получения будущих значений  требуется определить доверительный интервал возможных отклонений этих значений.
требуется определить доверительный интервал возможных отклонений этих значений.
Задача прогнозирования временного ряда с учетом одного внешнего фактора представлена на рисунке 1.3.
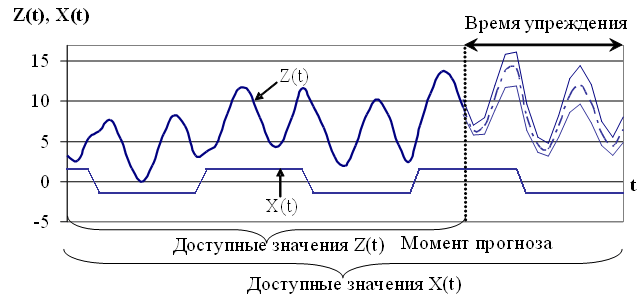
Рис. 1.3. Иллюстрация задачи прогнозирования временного ряда с учетом внешнего фактора
1.3. Обзор моделей прогнозирования
Перед тем как перейти к обзору моделей, необходимо отметить, что названия моделей и соответствующих методов как правило совпадают. Например, работы [1],[11], [12],[13] посвящены одной из самых распространенных моделей прогнозирования авторегрессия проинтегрированного скользящего среднего с учетом внешнего фактора (auto regression moving average external, ARIMAX). Эту модель и соответствующий ей метод обычно называют ARIMAX. В настоящее время принято использовать английские аббревиатуры названий как моделей, так и методов.
Набор понятных для чтения материалов по вопросу классификации моделей и методов прогнозирования временных рядов можно найти по тегу Классификация моделей прогнозирования.
Согласно работе [14], в настоящее время насчитывается свыше 100 классов моделей прогнозирования. Число общих классов моделей, которые в тех или иных вариациях повторяются в других, гораздо меньше. Часть моделей и соответствующих методов относится к отдельным процедурам прогнозирования. Часть методов представляет набор отдельных приемов, отличающихся от базовых или друг от друга количеством частных приемов и последовательностью их применения.
В аналитическом обзоре [14] все методы прогнозирования делятся на две группы: интуитивные и формализованные.
Об этом я подробнее говорю в записи Классификация методов прогнозирования по Э. Тихонову.
Интуитивное прогнозирование применяется тогда, когда объект прогнозирования либо слишком прост, либо, напротив, настолько сложен, что аналитически учесть влияние внешних факторов невозможно. Интуитивные методы прогнозирования не предполагают разработку моделей прогнозирования и отражают индивидуальные суждения специалистов (экспертов) относительно перспектив развития процесса. Интуитивные методы основаны на мобилизации профессионального опыта и интуиции. Такие методы используются для анализа процессов, развитие которых либо полностью, либо частично не поддается математической формализации, то есть для которых трудно разработать адекватную модель. В статье [6] указано, что к таким методам относятся методы экспертных оценок, исторических аналогий, предвидения по образцу. Кроме того, в настоящее время широко распространено применение экспертных систем, в том числе с использованием нечеткой логики [15]. В статье [16] подробно описаны интуитивные методы прогнозирования.
Формализованные методы рассматривают модели прогнозирования. В обзоре [9] модели прогнозирования разделяются на статистические модели и структурные модели.
Об этом я подробнее говорю в другой записи Классификация моделей прогнозирования временных рядов по Jingfei Yang.
В статистических моделях функциональная зависимость между будущими и фактическими значениями временного ряда, а также внешними факторами задана аналитически. К статистическим моделям относятся следующие группы:
- регрессионные модели;
- авторегрессионные модели;
- модели экспоненциального сглаживания.
В структурных моделях функциональная зависимость между будущими и фактическими значениями временного ряда, а также внешними факторами задана структурно. К структурным моделям относятся следующие группы:
- нейросетевые модели;
- модели на базе цепей Маркова;
- модели на базе классификационно-регрессионных деревьев.
Кроме того, необходимо отметить, что для узкоспециализированных задач иногда применяются особые модели прогнозирования. Так, например, для задачи прогнозирования уровня сахара крови человека применяются модели на основе дифференциальных уравнений [8]. Для задачи прогнозирования транспортного потока, которая в последние несколько лет актуальна для мегаполисов, применяются гидродинамические модели [17]. Для прогнозирования природных явлений, таких как землетрясения, применяется, например, модель, в основу которой положены нелинейные клетки (или соты), находящиеся под воздействием внешнего поля, и у которых есть внутреннее состояние, изменяющееся во времени под воздействием этого поля [18]. Аналогичные модели разрабатываются и применяются для специальных процессов и систем. В рамках настоящей работы данный класс формализованных моделей не рассматривается.
1.3.1. Регрессионные модели
Существует много задач, требующих изучения отношения между двумя и более переменными. Для решения таких задач используется регрессионный анализ [19]. В настоящее время регрессия получила широкое применение, включая задачи прогнозирования и управления. Целью регрессионного анализа является определение зависимости между исходной переменной и множеством внешних факторов (регрессоров). При этом коэффициенты регрессии могут определяться по методу наименьших квадратов [19] или методу максимального правдоподобия [20].
Линейная регрессионная модель. Самым простым вариантом регрессионной модели является линейная регрессия. В основу модели положено предположение, что существует дискретный внешний фактор X(t), оказывающий влияние на исследуемый процесс Z(t), при этом связь между процессом и внешним фактором линейна. Модель прогнозирования на основании линейной регрессии описывается уравнением
где α0 и α1 — коэффициенты регрессии; εt — ошибка модели. Для получения прогнозных значений Z(t) в момент времени t необходимо иметь значение X(t) в тот же момент времени t, что редко выполнимо на практике.
Множественная регрессионная модель. На практике на процесс Z(t) оказывают влияние целый ряд дискретных внешних факторов X1(t),…,XS(t). Тогда модель прогнозирования имеет вид
Недостатком данной модели является то, что для вычисления будущего значения процесса Z(t) необходимо знать будущие значения всех факторов X1(t),…,XS(t), что почти невыполнимо на практике.
В основу нелинейной регрессионной модели положено предположение о том, что существует известная функция, описывающая зависимость между исходным процессом Z(t) и внешним фактором X(t)
В рамках построения модели прогнозирования необходимо определить параметры функции A. Например, можно предположить, что
Для построения модели достаточно определить параметры 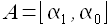 . Однако на практике редко встречаются процессы, для которых вид функциональной зависимости между процессом Z(t) и внешним фактором X(t) заранее известен. В связи с этим нелинейные регрессионные модели применяются редко.
. Однако на практике редко встречаются процессы, для которых вид функциональной зависимости между процессом Z(t) и внешним фактором X(t) заранее известен. В связи с этим нелинейные регрессионные модели применяются редко.
Модель группового учета аргументов (МГУА) была разработана Ивахтенко А.Г. [21]. Модель имеет вид
Уравнение (1.9) называется опорной функцией. Используя опорную функцию, строят различные варианты моделей для некоторых или всех аргументов. Например, строятся полиномы с одной переменной, полиномы со всевозможными парами переменных, полиномы со всевозможными тройками переменных и т.д. Для каждой модели определяются её линейные коэффициенты αi,j,k,... методом регрессионного анализа. Среди всех моделей выбираются несколько (от 2 до 10) наилучших. При этом качество моделей определяется, например, среднеквадратичным отклонением или иным критерием. Если среди выбранных имеется модель, качество которой достаточно для использования полученных прогнозных значений, то процесс перебора моделей прекращается. Иначе отобранные модели используются в качестве аргументов X1(t),…,XS(t) для опорных функций следующего этапа итерации. То есть уже найденные модели участвуют в формировании более сложных.
1.3.2. Авторегрессионные модели
Самая популярная модель данного класса - ARIMAX рассмотрена мною подробно в наборе записей по соответствующему тэгу ARIMAX.
В основу авторегрессионных моделей заложено предположение о том, что значение процесса Z(t) линейно зависит от некоторого количества предыдущих значений того же процесса Z(t-1),…,Z(t-p).
Авторегрессионная модель скользящего среднего. В области анализа временных рядов модель авторегрессии (autoregressive, AR) и модель скользящего среднего (moving average, MA) является одной из наиболее используемых [1],[5].
Согласно работе [1], модель авторегрессии является исключительно полезной для описания некоторых встречающихся на практике временных рядов. В этой модели текущее значение процесса выражается как конечная линейная совокупность предыдущих значений процесса и импульса, который называется «белым шумом»,
Формула (1.10) описывает процесс авторегреcсии порядка p, который в литературе часто обозначается AR(p), здесь C — вещественная константа, φ1,..,φp — коэффициенты, εt — ошибка модели. Для определения φi и C используют метод наименьших квадратов [19] или метод максимального правдоподобия [20].
Другой тип модели имеет большое значение в описании временных рядов и часто используется совместно с авторегрессией называется моделью скользящего среднего порядка q и описывается уравнением
В литературе процесс (1.11) часто обозначается MA(q); здесь q — порядок скользящего среднего, εt — ошибка прогнозирования. Модель скользящего среднего является по сути дела фильтром низких частот. Нужно отметить, что существуют простые, взвешенные, кумулятивные, экспоненциальные модели скользящего среднего.
Согласно работе [1], для достижения большей гибкости в подгонке модели часто целесообразно объединить в одной модели авторегрессию и скользящее среднее. Общая модель обозначается ARMA(p,q) соединяет в себе фильтр в виде скользящего среднего порядка q и авторегрессию фильтрованных значений процесса порядка p.
Если в качестве входных данных используются не сами значения временного ряда, а их разность d-того порядка (на практике d необходимо определять, однако в большинстве случаев d ≤ 2), то модель носит название авторгерессии проинтегрированного скользящего среднего. В литературе данную модель называют ARIMA(p,d,q) (autoregression integrated moving average).
Развитием модели ARIMA(p,d,q) является модель ARIMAX(p,d,q), которая описывается уравнением
Здесь α1,...,αS — коэффициенты внешних факторов X1(t),…,XS(t). В данной модели чаще всего процесс Z(t) является результатом модели MA(q), то есть отфильтрованными значениями исходного процесса. Далее для прогнозирования Z(t) используется модель авторегрессии, в которой введены дополнительные регрессоры внешних факторов X1(t),…,XS(t).
Авторегрессионная модель с условной гетероскедастичностью (autoregressive conditional heteroskedasticity, GARCH) была разработана в 1986 году Тимом Петером Борреслевом и является моделью остатков для модели AR(p) [22]. На первом этапе для исходного временного ряда определяется модель AR(p) (1.10). Далее предполагается, что ошибка модели (1.10) εt имеет две составляющие
где σt — зависимое от времени стандартное отклонение; ςt — случайная величина, имеющая нормальное распределение, среднее значение, равное 0, и стандартное отклонение, равное 1. При этом зависимое от времени стандартное отклонение описывается уравнением
Здесь β0,...,βq и γ0,..., γp — коэффициенты. Уравнение (1.14) называется моделью GARCH(p,q) и имеет два параметра: p характеризует порядок авторегрессии квадратов остатков; q — количество предшествующих оценок остатков.
Наиболее частое применение данная модель получила в финансовом секторе, где с помощью нее моделируется волатильность. На сегодняшний день существует ряд модификаций модели под названиями NGARCH, IGARCH, EGARCH, GARCH-M и другие [22].
Авторегрессионнная модель с распределенным лагом (autoregressive distributed lag models, ARDLM) недостаточно подробно описана в литературе. Основное внимание данной модели уделяется в книгах по эконометрике [23].
Часто при моделировании процессов на изучаемую переменную влияют не только текущие значения процесса, но и его лаги, то есть значения временного ряда, предшествующие изучаемому моменту времени. Модель авторегрессии распределенного лага описывается уравнением
Здесь φ0,..., φp — коэффициенты, l — величина лага. Модель (1.15) называется ARDLM(p,l) и чаще всего применяется для моделирования экономических процессов [23].
1.3.3. Модели экспоненциального сглаживания
Примеры реализации экспоненциального сглаживания можно найти по тэгу Экспоненциальное сглаживание.
Модели экспоненциального сглаживания разработаны в середине XX века и до сегодняшнего дня являются широко распространенными в силу их простоты и наглядности.
Модель экспоненциального сглаживания (exponential smoothing, ES) применяется для моделирования финансовых и экономических процессов [24]. В основу экспоненциального сглаживания заложена идея постоянного пересмотра прогнозных значений по мере поступления фактических. Модель ES присваивает экспоненциально убывающие веса наблюдениям по мере их старения. Таким образом, последние доступные наблюдения имеют большее влияние на прогнозное значение, чем старшие наблюдения.
Функция модели ES имеет вид
где α — коэффициент сглаживания, 0 < α < 1; начальные условия определяются как S(1) = Z(0). В данной модели каждое последующее сглаженное значение S(t) является взвешенным средним между предыдущим значением временного ряда Z(t) и предыдущего сглаженного значения S(t-1).
Модель Хольта или двойное экспоненциальное сглаживание применяется для моделирования процессов, имеющих тренд. В этом случае в модели необходимо рассматривать две составляющие: уровень и тренд [24]. Уровень и тренд сглаживаются отдельно
Здесь α — коэффициент сглаживания уровня, как и в модели (1.16), γ — коэффициент сглаживания тренда.
Модель Хольта-Винтерса или тройное экспоненциальное сглаживание применяется для процессов, которые имеют тренд и сезонную составляющую
Здесь R(t) — сглаженный уровень без учета сезонной составляющей
G(t) — сглаженный тренд
а S(t) — сезонная составляющая
Величина L определяется длиной сезона исследуемого процесса. Модели экспоненциального сглаживания наиболее популярны для долгосрочного прогнозирования.
1.3.4. Нейросетевые модели
Набор читабельных материалов с примерами реализации нейронных сетей можно найти по тэгу Нейронные сети
В настоящее время самой популярной среди структурных моделей является модель на основе искусственных нейронных сетей (artificial neural network, ANN) [5]. Нейронные сети состоят из нейронов (рис 1.4.).
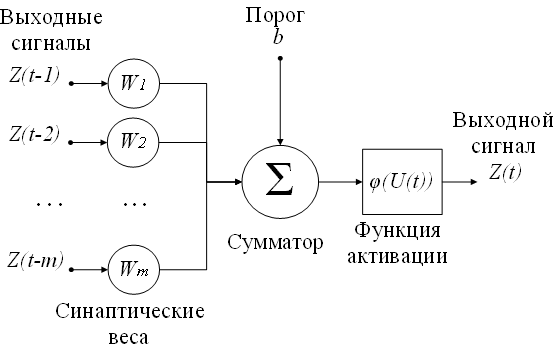
Рис. 1.4. Нелинейная модель нейрона
Модель нейрона можно описать парой уравнений
где Z(t-1),...,Z(t-m) — входные сигналы; ω1,...,ωm — синаптические веса нейрона; p — порог; φ(U(t)) — функция активации.
Функция активации бывают трех основных типов [25]:
- функция единичного скачка;
- кусочно-линейная функция;
- сигмоидальная функция.
Способ связи нейронов определяет архитектуру нейронной сети. Согласно работе [25], в зависимости от способа связи нейронов сети делятся на
- однослойные нейронные сети прямого распространения,
- многослойные нейронные сети прямого распространения,
- рекуррентные нейронные сети.
На рисунке 1.5 представлена структура трехслойной нейронной сети прямого распространения, применяемая для прогнозирования в работах [26],[27],[28],[29].
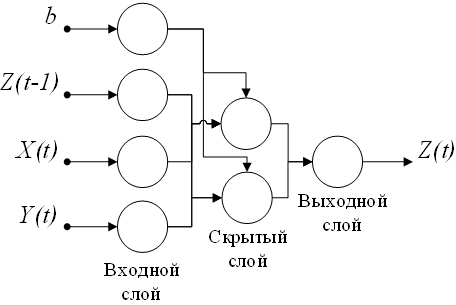
Рис. 1.5. Трехслойная нейронная сеть прямого распространения
Таким образом, при помощи нейронных сетей возможно моделирование нелинейной зависимости будущего значения временного ряда от его фактических значений и от значений внешних факторов. Нелинейная зависимость определяется структурой сети и функцией активации.
Пример реализации в MATLAB трехслойной нейронной сети для прогнозирования энергопотребоения на 24 значения вперед можно найти в записи блога Создаем нейронную сеть для прогнозирования временного ряда.
1.3.5. Модели на базе цепей Маркова
Модели прогнозирования на основе цепей Маркова (Markov chain model) предполагают, что будущее состояние процесса зависит только от его текущего состояния и не зависит от предыдущих [30]. В связи с этим процессы, моделируемые цепями Маркова, должны относиться к процессами с короткой памятью.
Пример цепи Маркова для процесса, имеющего три состояния, представлен на рис. 1.6.
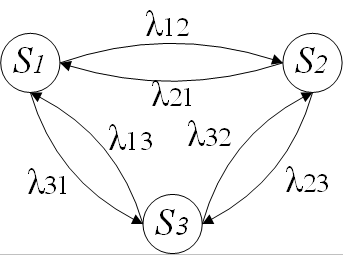
Рис. 1.6. Цепь Маркова с тремя состояниями
Здесь S1,...,X3 — состояния процесса Z(t); λ12 — вероятность перехода из состояния S1 в состояние S2, λ23 — вероятность перехода из состояния S2 в состояние S3 и т.д. При построении цепи Маркова определяется множество состояний и вероятности переходов. Есть текущее состояние процесса Si, то качестве будущего состояния процесса выбирается такое состояние Si, вероятность перехода в которое (значение λij) максимальна.
Таким образом, структура цепи Маркова и вероятности перехода состояний определяют зависимость между будущим значением процесса и его текущим значением.
1.3.6. Модели на базе классификационно-регрессионных деревьев
Классификационно-регрессионные деревья (classification and regression trees, CART) являются еще одной популярной структурной моделью прогнозирования временных рядов [31]. Структурные модели CART разработаны для моделирования процессов, на которые оказывают влияние как непрерывные внешние факторы, так и категориальные. Если внешние факторы, влияющие на процесс Z(t), непрерывны, то используются регрессионные деревья; если факторы категориальные, то — классификационные деревья. В случае, если необходимо учитывать факторы обоих типов, то используются смешанные классификационно-регрессионные деревья.
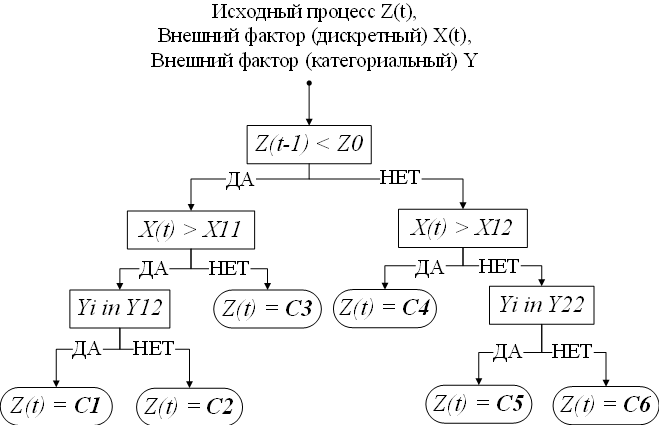
Рис. 1.7. Бинарное классификационно-регрессионное дерево
Согласно модели CART, прогнозное значение временного ряда зависит от предыдущих значений, а также некоторых независимых переменных. На приведенном на рисунке 1.7 примере сначала предыдущее значение процесса сравнивается с константой Z0. Если значение Z(t-1) меньше Z0, то выполняется следующая проверка: X(t) > X11. Если неравенство не выполняется, то Z(t) = C3, иначе проверки продолжаются до того момента, пока не будет найден лист дерева, в котором происходит определение будущего значения процесса Z(t). Важно, что при определении значения в расчет принимаются как непрерывные переменные, например, X(t), так и категориальные Y, для которых выполняется проверка присутствия значения в одном из заранее определенных подмножеств. Значения пороговых констант, например, Z0, X11, а также подмножеств Y11,Y12 выполняется на этапе обучения дерева [31].
Таким образом, CART моделирует зависимость будущей величины процесса Z(t) при помощи структуры дерева, а также пороговых констант и подмножеств.
1.1.1. Другие модели и методы прогнозирования
Кроме классов моделей прогнозирования, рассмотренных выше, существуют менее распространенные модели и методы прогнозирования. Главным недостатком моделей и методов, упомянутых в настоящем разделе, является недостаточная методологическая база, т. е. недостаточно подробное описание возможностей как моделей, так и путей определения их параметров. Кроме того, в открытом доступе можно найти лишь небольшое количество статей, посвященных применению данных методов.
Метод опорных векторов (support vector machine, SVM) применяется, например, для прогнозирования движения рынков [32] и цен на электроэнергию [5]. В основу метода положена классификация, производимая за счет перевода исходных временных рядов, представленных в виде векторов, в пространство более высокой размерности и поиска разделяющей гиперплоскости с максимальным зазором в этом пространстве. Алгоритм SVM работает в предположении, что чем больше разница или расстояние между этими параллельными гиперплоскостями, тем меньше будет средняя ошибка классификатора [33]. При этом задача прогнозирования решается таким образом, что на этапе обучения классификатора выявляются независимые переменные (внешние факторы), будущие значения которых определяют в какой из определенных ранее подклассов попадет прогноз Z(t).
Генетический алгоритм (genetic algorithm, GA) был разработан и часто применяется для решения задач оптимизации, а также поисковых задач. Однако некоторые модификации GA позволяют решать задачи прогнозирования.
В статье [34] указано, что алгоритм прогнозирования на основе GA позволяет принимать в расчет более 15 внешних факторов, используя базовый GA. Принцип работы основан на том, что исходные значения процесса Z(t) и внешних факторов X1(t),…,XS(t) раскладывают в наборы, состоящие из 0 и 1, которые называют генотипами. Далее применяют ряд преобразований: скрещивание и мутирование для формирования преобразованных наборов, которые называются фенотипами. Исходные и полученные наборы исследуются с использованием функции приспособленности. Если решение получилось неудовлетворительным, то снова производится скрещивание и мутирование, в результате чего получается еще более новые наборы (новое поколение), которые снова оцениваются. Итеративный процесс продолжается до тех пор, пока решение не будет удовлетворительным.
Модель на основе передаточных функций (transfer function, TF) применяется для прогнозирования процесса Z(t) с учетом внешнего фактора X(t) [35]. Уравнение, отражающее зависимость будущего значения имеет вид
где B — оператор сдвига BZ(t) = Z(t-1),…,BkZ(t) =Z(t-k). Временной ряд η(t) характеризует внешнее возмущение. При этом функция ν(B) имеет вид
Коэффициенты функции (1.24) νi описывают динамические отношения между процессами Z(t) и X(t).
1.4. Сравнение моделей прогнозирования
В предыдущем разделе представлен обзор существующих моделей прогнозирования. В настоящем разделе рассмотрены преимущества и недостатки не только описанных выше моделей, но и методов. Говоря о достоинствах и недостатках моделей прогнозирования, необходимо принимать во внимание и соответствующие им методы.
1.4.1. Достоинства и недостатки моделей
Регрессионные модели и методы. К достоинствам данных моделей прогнозирования относят простоту, гибкость, а также единообразие их анализа и проектирования [19]. При использовании линейных регрессионных моделей результат прогнозирования может быть получен быстрее, чем при использовании остальных моделей. Кроме того, достоинством является прозрачность моделирования [5], т. е. доступность для анализа всех промежуточных вычислений.
Основным недостатком нелинейных регрессионных моделей является сложность определения вида функциональной зависимости [14], а также трудоемкость определение параметров модели. Недостатками линейных регрессионных моделей являются низкая адаптивность и отсутствие способности моделирования нелинейных процессов [28].
Авторегрессионные модели и методы. Важными достоинствами данного класса моделей являются их простота и прозрачность моделирования. Еще одним достоинством является единообразие анализа и проектирования, заложенное в работе [1]. На сегодняшний день данный класс моделей является одним из наиболее популярных [3], а потому в открытом доступе легко найти примеры применения авторегрессионных моделей для решения задач прогнозирования временных рядов различных предметных областей.
Недостатками данного класса моделей являются: большое число параметров модели, идентификация которых неоднозначна и ресурсоемка [4]; низкая адаптивность моделей, а также линейность и, как следствие, отсутствие способности моделирования нелинейных процессов, часто встречающихся на практике [26].
Модели и методы экспоненциального сглаживания. Достоинствами данного класса моделей являются простота и единообразие их анализа и проектирования. Данный класс моделей чаще других используется для долгосрочного прогнозирования [24].
Недостатком данного класса моделей прогнозирования является отсутствие гибкости [36].
Нейросетевые модели и методы. Основным достоинством нейросетевых моделей является нелинейность, т.е. способность устанавливать нелинейные зависимости между будущими и фактическими значениями процессов. Другими важными достоинствами являются: адаптивность, масштабируемость (параллельная структура ANN ускоряет вычисления) и единообразие их анализа и проектирования [25].
При этом недостатками ANN являются отсутствие прозрачности моделирования; сложность выбора архитектуры, высокие требования к непротиворечивости обучающей выборки; сложность выбора алгоритма обучения и ресурсоемкость процесса их обучения [5].
Модели и методы на базе цепей Маркова. Простота и единообразие анализа и проектирования являются достоинствами моделей на базе цепей Маркова.
Недостатком данных моделей является отсутствие возможности моделирования процессов с длинной памятью [30].
Модели на базе классификационно-регрессионных деревьев. Достоинствами данного класса моделей являются: масштабируемость, за счет которой возможна быстрая обработка сверхбольших объемов данных; быстрота и однозначность процесса обучения дерева (в отличие от ANN) [9], а также возможность использовать категориальные внешние факторы.
Недостатками данных моделей являются неоднозначность алгоритма построения структуры дерева; сложность вопроса останова т.е. вопроса о том, когда стоит прекратить дальнейшие ветвления; отсутствие единообразия их анализа и проектирования [31].
Достоинства и недостатки моделей и методов систематизированы в таблице 1.
Таблица 1. Сравнение моделей и методов прогнозирования
| Модель и метод | Достоинства | Недостатки |
|---|---|---|
| Регрессионные модели и методы | простота, гибкость, прозрачность моделирования; единообразие анализа и проектирования | сложность определения функциональной зависимости; трудоемкость нахождения коэффициентов зависимости; отсутствие возможности моделирования нелинейных процессов (для нелинейной регрессии) |
| Авторегрессионные модели и методы | простота, прозрачность моделирования; единообразие анализа и проектирования; множество примеров применения | трудоемкость и ресурсоемкость идентификации моделей; невозможность моделирования нелинейностей; низкая адаптивность |
| Модели и методы экспоненциального сглаживания | простота моделирования; единообразие анализа и проектирования | недостаточная гибкость; узкая применимость моделей |
| Нейросетевые модели и методы | нелинейность моделей; масштабируемость, высокая адаптивность; единообразие анализа и проектирования; множество примеров применения | отсутствие прозрачности; сложность выбора архитектуры; жесткие требования к обучающей выборке; сложность выбора алгоритма обучения; ресурсоемкость процесса обучения |
| Модели и методы на базе цепей Маркова | простота моделирования; единообразие анализа и проектирования | невозможность моделирования процессов с длинной памятью; узкая применимость моделей |
| Модели и методы на базе классификационно-регрессионных деревьев | масштабируемость; быстрота и простота процесса обучения; возможность учитывать категориальные переменные | неоднозначность алгоритма построения дерева; сложность вопроса останова |
Нужно дополнительно отметить, что ни для одной из рассмотренных групп моделей (и методов) в достоинствах не указана точность прогнозирования. Это сделано в связи с тем, что точность прогнозирования того или иного процесса зависит не только от модели, но и от опыта исследователя, от доступности данных, от располагаемой аппаратной мощности и многих других факторов. Точность прогнозирования будет оцениваться для конкретных задач, решаемых в рамках данной работы.
В ряде работ [2],[36],[37] указано, что на сегодняшний день наиболее распространенными моделями прогнозирования являются авторегрессионные модели (ARIMAX), а также нейросетевые модели (ANN). В статье [3], в частности, утверждается: «Without a doubt ARIMA(X) and GRACH modeling methodologies are the most popular methodologies for forecasting time series. Neural networks are now the biggest challengers to conventional time series forecasting methods». (Без сомнений модели ARIMA(X) и GARCH являются самыми популярными для прогнозирования временных рядов. В настоящее время главную конкуренцию данным моделям составляют модели на основе ANN.)
1.4.2. Комбинированные модели
Одной из популярных современных тенденций в области создания моделей прогнозирования является создание комбинированных моделей и методов. Подобный подход дает возможность компенсировать недостатки одних моделей при помощи других и направлен на повышение точности прогнозирования, как одного из главных критериев эффективности модели.
Одной из первых работ в этой области является статья [38]. В ней предлагается подход, в котором прогнозирование временного ряда осуществляется в два этапа. На первом этапе на основании моделей распознавания образов (pattern recognition) выделяются гомогенные группы (patterns) временного ряда. На следующем этапе для каждой группы строится отдельная модель прогнозирования. В статье указывается, что при комбинированном подходе удается повысить точность прогнозирования временных рядов.
В работе [13] предлагается модель для прогнозирования цен на электроэнергию Испании. При помощи вейвлет преобразования (wavelet transform) доступные значения временного ряда разделяются на несколько последовательностей, для каждой из которых строится отдельная модель ARIMA.
В обзоре моделей прогнозирования энергопотребления [36] рассматривается следующие типы комбинаций:
- нейронные сети + нечеткая логика;
- нейронные сети + ARIMA;
- нейронные сети + регрессия;
- нейронные сети + GA + нечеткая логика;
- регрессия + нечеткая логика.
В большинстве комбинаций модели на основе нейронных сетей применяются для решения задачи кластеризации, а далее для каждого кластера строиться отдельная модель прогнозирования на основе ARIMA, GA, нечеткой логики и др. В работе утверждается, что применение комбинированных моделей, выполняющих предварительную кластеризации и последующее прогнозирование внутри определенного кластера, является наиболее перспективным направлением развития моделей прогнозирования.
Работа [39] посвящена вопросам кластеризации временных рядов для того, чтобы на основании полученных кластеров выполнять прогнозирование. Для кластеризации предлагается два метода: метод K- cредних (K-mean) и метод нечетких C-средних (fuzzy C-mean). Целью обоих алгоритмов кластеризации является извлечение полезной информации из временного ряда для последующего прогнозирования. Авторы утверждают, что применение кластеризации дает возможность повысить точность прогнозирования.
Применение комбинированных моделей является направлением, которое при корректном подходе позволяет повысить точность прогнозирования. Главным недостатком комбинированных моделей является сложность и ресурсоемкость их разработки: нужно разработать модели таким образом, чтобы компенсировать недостатки каждой из них, не потеряв достоинств.
Ряд исследователей пошли по альтернативному пути и разработали авторегрессионные модели, в основе которых лежит предположение о том, что временной ряд есть последовательность повторяющихся кластеров (patterns). Однако при этом разработчики не создавали комбинированных моделей, а определяли кластеры и выполняли прогноз на основании одной модели. Рассмотрим эти модели подробнее.
В работе [40] предложена модель прогнозирования направления движения индексов рынка (index movement), учитывающая кластеры временного ряда. Пусть временной ряд содержит три значения -1, 0 и 1, которые характеризуют спад, стабильное состояние и подъем рынка соответственно. Кластером (pattern) называется последовательность 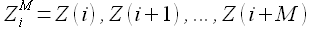 для i = 1,2,...,N-M, где N — число доступных отчетов временного ряда Z(t). Для определения прогнозного значения рассмотрена последняя доступная информация, а именно последовательность Z(N,M) = Z(N-M+1),Z(N-M+2),...,Z(N), для которой определена ближайшая похожая (closet match) Z(Q,M) = Z(Q+1),Z(Q+2),...,Z(Q+M). При этом функция, определяющая близость, имеет вид
для i = 1,2,...,N-M, где N — число доступных отчетов временного ряда Z(t). Для определения прогнозного значения рассмотрена последняя доступная информация, а именно последовательность Z(N,M) = Z(N-M+1),Z(N-M+2),...,Z(N), для которой определена ближайшая похожая (closet match) Z(Q,M) = Z(Q+1),Z(Q+2),...,Z(Q+M). При этом функция, определяющая близость, имеет вид
т.е. близость кластеров определяется простым сравнением. Далее вычисляется прогнозное значение
Таким образом, в данной модели предполагается, что если в некоторый момент времени в прошлом рынок вел себя определенным образом, то в будущем его поведение повторится в связи с тем, что временной ряд является последовательностью кластеров.
Еще в двух работах [41],[42] предложена модель прогнозирования, основанная на модели авторегрессии, но принимающая во внимание кусочки временного ряда. Здесь прогнозное значение временного ряда определено выражением
которое является линейной авторегрессией порядка M. При этом коэффициенты авторегрессии α0,α1,…,αM определяются следующим образом. Предполагается, что существует K кусочков (векторов) длины M временного ряда, для которых выполняется выражение
При определении ближайших векторов (closest vectors) Z(i1-1),Z(i1-2),…,Z(i1-M),...,Z(iK-1),Z(iK-2),…,Z(iK-M) в статье [41] использовано значение линейной корреляции Пирсона между всеми возможными векторами и новейшим вектором (last available vector) Z(t-1),Z(t-2),…,Z(t-M); а в статье [42] вместо линейной корреляции рассчитывается евклидово расстояние между векторами.
Отметим, что существует путаница в терминологии: в статье [41] использован термин pieces (кусочки), в статьях [4],[42] — термин vector, set (вектор, выборка); в работе [40] для аналогичного понятия использован термин pattern (выборка, кластер). В настоящей работе используем термин выборка (pattern) [40]. Англицизм паттерн в русском языке чаще применяется для описания задач классификации, например, в работе [43], а также кластеризации и распознавания образов (pattern recognition) [44].
Разработчики рассмотренных выше моделей утверждают, что предложенные модели просты, прозрачны и эффективны для исследованных временных рядов. При этом очевидно, что главными недостатками данных моделей являются:
- невозможность учитывать внешние факторы;
- неоднозначность критерия определения похожей выборки;
- сложность определения эффективной комбинации двух параметров M (длина векторов) и K (число векторов, принимаемых в расчет) в работах [41],[42].
В рамках диссертации установлено, что подход, предложенный авторами работ [40],[41],[42], является перспективным в области создания моделей прогнозирования временных рядов. Предложенная в диссертации модель прогнозирования развивает модели [40],[41],[42] и устраняет все перечисленные выше недостатки: модель позволяет учитывать влияния внешних факторов; формулируется критерий определения похожей выборки для двух видов постановок задачи прогнозирования (1.11); количество параметром модели сокращается до одного, что существенно упрощает идентификацию модели.
1.5. Выводы
1) Задача прогнозирования временных рядов имеет высокую актуальность для многих предметных областей и является неотъемлемой частью повседневной работы многих компаний.
2) Установлено, что к настоящему времени разработано множество моделей для решения задачи прогнозирования временного ряда, среди которых наибольшую применимость имеют авторегрессионные и нейросетевые модели.
3) Выявлены достоинства и недостатки рассмотренных моделей. Установлено, что существенным недостатком авторегрессионных моделей является большое число свободных параметров, требующих идентификации; недостатками нейросетевых моделей является ее непрозрачность моделирования и сложность обучения сети.
4) Определено, что наиболее перспективным направлением развития моделей прогнозирования с целью повышения точности является создание комбинированных моделей, выполняющих на первом этапе кластеризацию, а затем прогнозирование временного ряда внутри установленного кластера.
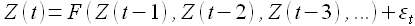 (1.1)
(1.1)
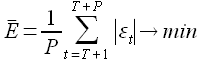 (1.2)
(1.2)
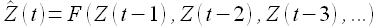 (1.3)
(1.3)
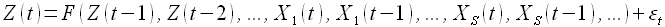 (1.4)
(1.4)
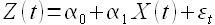 (1.5)
(1.5)
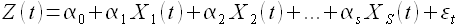 (1.6)
(1.6)
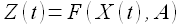 (1.7)
(1.7)
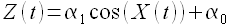 (1.8)
(1.8)
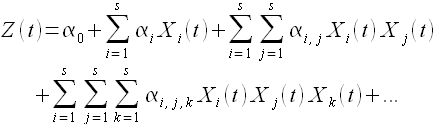 (1.9)
(1.9)
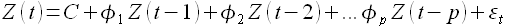 (1.10)
(1.10)
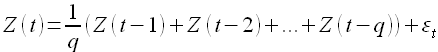 (1.11)
(1.11)
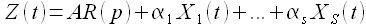 (1.12)
(1.12)
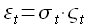 (1.13)
(1.13)
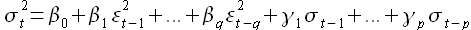 (1.14)
(1.14)
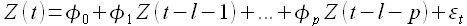 (1.15)
(1.15)
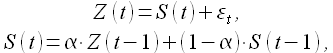 (1.16)
(1.16)
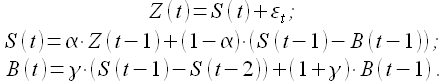 (1.17)
(1.17)
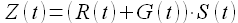 (1.18)
(1.18)
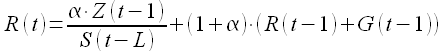 (1.19)
(1.19)
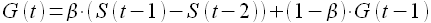 (1.20)
(1.20)
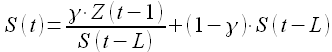 (1.21)
(1.21)
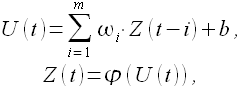 (1.22)
(1.22)
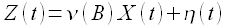 (1.23)
(1.23)
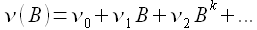 (1.24)
(1.24)
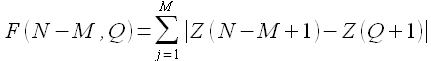 (1.25)
(1.25)
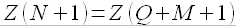 (1.26)
(1.26)
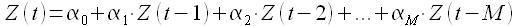 (1.27)
(1.27)
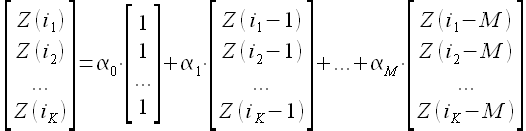 (1.28)
(1.28)